
【题目】如图,直线![]() 与顶点为
与顶点为![]() 的抛物线
的抛物线![]() 的交点
的交点![]() 在
在![]() 轴上,交点
轴上,交点![]() 在
在![]() 轴上.
轴上.
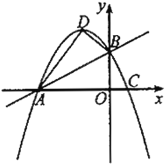
(1)求抛物线的解析式.
(2)![]() 是否为直角三角形,请说明理由.
是否为直角三角形,请说明理由.
(3)在第二象限的抛物线上,是否存在异于顶点的点![]() ,使
,使![]() 与
与![]() 的面积相等?若存在,求出符合条件的
的面积相等?若存在,求出符合条件的![]() 点坐标.若不存在,请说明理由.
点坐标.若不存在,请说明理由.
(4)在第三象限的抛物线上求出点![]() ,使
,使![]() .
.
【答案】(1)![]() ;(2)不是直角三角形,理由见解析;(3)存在,
;(2)不是直角三角形,理由见解析;(3)存在,![]() ;(4)点
;(4)点![]() .
.
【解析】
(1)待定系数法即可求出;
(2)取![]() 中点
中点![]() ,根据点的坐标关系判断
,根据点的坐标关系判断![]() 即可证明;
即可证明;
(3)设![]() 的解析式为
的解析式为![]() ,代入D点坐标可求出,通过解方程
,代入D点坐标可求出,通过解方程![]() ,若有解,即可证明存在;
,若有解,即可证明存在;
(4)设直线![]() 的解析式为
的解析式为![]() 并求出,进而可求出直线
并求出,进而可求出直线![]() 的解析式,联立BF与抛物线解析式即可求得.
的解析式,联立BF与抛物线解析式即可求得.
解:(1)如图,

由![]() 知,
知,![]() ,
,![]() .
.
则抛物线![]() .
.
将![]() 代入,得
代入,得![]() .
.
∴![]() .
.
∴抛物线解析式为![]() .
.
(2)![]() 不是直角三角形.理由如下
不是直角三角形.理由如下
由(1),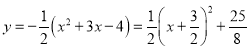 ,
,
∴顶点![]() .
.
如图,由(1),可得![]() .
.
取![]() 中点
中点![]() .
.
则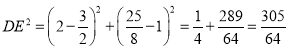 .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() 不是直角三角形.
不是直角三角形.
(3)如图,存在点![]() ,使
,使![]() .
.
设经过点![]() 与
与![]() 平行的直线
平行的直线![]() 的解析式为
的解析式为![]() .
.
将![]() 代入,得
代入,得![]() .∴
.∴![]() .
.
∴![]() 的解析式为
的解析式为![]() .
.
由![]() ,整理,得
,整理,得![]() .
.
解得![]() ,
,![]() .
.
当![]() 时,
时,![]() .
.
∴![]() .
.
(4)如图,设直线![]() 的解析式为
的解析式为![]() .
.
则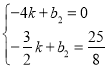 解得
解得![]() ,
,![]() .
.
∴直线![]() 的解析式为
的解析式为![]() .
.
∴经过点![]() 与
与![]() 平行的直线
平行的直线![]() 的解析式为
的解析式为![]() .
.
由![]() ,整理,得
,整理,得![]() .
.
解得![]() ,或
,或![]() .
.
当![]() 时,
时,![]() .
.
∴抛物线上点![]() ,满足
,满足![]() .
.


科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境卫生,垃圾分类开始实施.我市为了促进生活垃圾的分类处理,将生活垃圾分为“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”四类,并且设置了相应的垃圾箱.

(1)小亮将妈妈分类好的某类垃圾随机投入到四种垃圾箱某类箱内,请写出小亮投放正确的概率为 ;
(2)经过妈妈的教育,小明已经分清了“有害垃圾”,但仍然分不清“可回收物”、“湿垃圾”和“干垃圾”,这天小亮要将妈妈分类好的四类垃圾投入到四种垃圾箱内,请求出小明投放正确的概率;
(3)请你就小亮投放垃圾的事件提出两条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
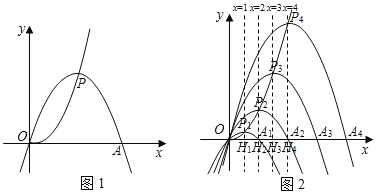
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.
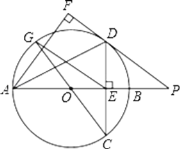
(1)求证:DF是⊙O的切线;
(2)求证:OC2=OEOP;
(3)求线段EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
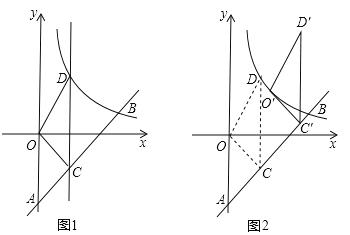
【题目】(2016江苏省镇江市) (2016镇江)如图1,一次函数y=kx﹣3(k≠0)的图象与y轴交于点A,与反比例函数![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上的动点(于点A、B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求△OCD面积的最大值;
(3)将(2)中面积取得最大值的△OCD沿射线AB方向平移一定的距离,得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上(如图2),则点D′的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上任意一点,
上任意一点,![]() 是等边三角形,且点
是等边三角形,且点![]() 在
在![]() 的内部,连接
的内部,连接![]() .探究线段
.探究线段![]() 与
与![]() 之间的数量关系.
之间的数量关系.
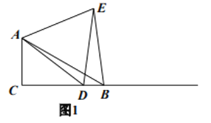
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
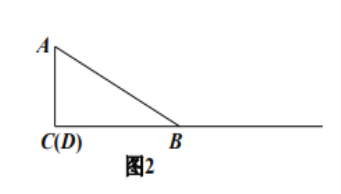
![]() 当点
当点![]() 与点
与点![]() 重合时(如图2),请你补全图形.由
重合时(如图2),请你补全图形.由![]() 的度数为_______________,点
的度数为_______________,点![]() 落在_______________,容易得出
落在_______________,容易得出![]() 与
与![]() 之间的数量关系为_______________
之间的数量关系为_______________
![]() 当
当![]() 是
是![]() 的平分线时,判断
的平分线时,判断![]() 与
与![]() 之间的数量关系并证明
之间的数量关系并证明
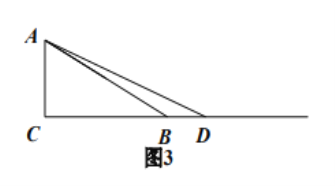
![]() 当点
当点![]() 在如图3的位置时,请你画出图形,研究
在如图3的位置时,请你画出图形,研究![]() 三点是否在以
三点是否在以![]() 为圆心的同一个圆上,写出你的猜想并加以证明.
为圆心的同一个圆上,写出你的猜想并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点![]() .甲从中山路上点
.甲从中山路上点![]() 出发,骑车向北匀速直行;与此同时,乙从点
出发,骑车向北匀速直行;与此同时,乙从点![]() 出发,沿北京路步行向东匀速直行.设出发
出发,沿北京路步行向东匀速直行.设出发![]() 时,甲、乙两人与点
时,甲、乙两人与点![]() 的距离分别为
的距离分别为![]() 、
、![]() .已知
.已知![]() 、
、![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
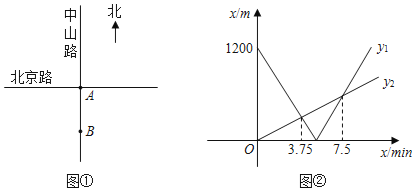
(1)求甲、乙两人的速度;
(2)当![]() 取何值时,甲、乙两人之间的距离最短?
取何值时,甲、乙两人之间的距离最短?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com