
分析 (1)根据题意可得房间每天的入住量=60个房间-每个房间每天的定价增加的钱数÷10;
(2)支出费用为20×(60-$\frac{x}{10}$),则利润w=(200+x)(60-$\frac{x}{10}$)-20×(60-$\frac{x}{10}$);
(3)利用配方法化简可求最大值.
解答 解:(1)由题意得:
y=60-$\frac{x}{10}$;
(2)w=(200+x)(60-$\frac{x}{10}$)-20×(60-$\frac{x}{10}$)=$-\frac{1}{10}{x}^{2}$+42x+10800
(3)w=$-\frac{1}{10}{x}^{2}$+42x+10800
=$-\frac{1}{10}{x}^{2}$+42x+10800
=-$\frac{1}{10}$(x-210)2+15210
当x=210时,w有最大值.
此时,x+200=410,就是说,当每个房间的定价为每天410元时,w有最大值,且最大值是15210元.
点评 此题考查二次函数的应用,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题主要考查的是二次函数的应用,难度一般.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
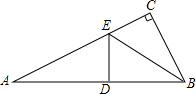 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
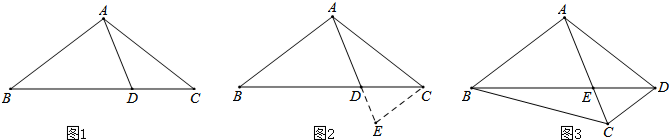
 如图,矩形纸片ABCD中,AB=4cm,BC=8cm,现将A、C重合,使纸片折叠压平,设折痕为EF,
如图,矩形纸片ABCD中,AB=4cm,BC=8cm,现将A、C重合,使纸片折叠压平,设折痕为EF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠-$\frac{1}{2}$ | B. | x≠$\frac{1}{2}$ | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com