
ΓΨΧβΡΩΓΩBΘ§C «Γ―O…œΒΡΝΫΗωΕ®ΒψΘ§A «‘≤…œΒΡΕ·ΒψΘ§0ΓψΘΦΓœBACΘΦ90ΓψΘ§BDΓΈACΘ§CDΓΈABΘ°
Θ®1Θ©»γΆΦ1Θ§»γΙϊΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§«σ÷ΛBD «Γ―OΒΡ«–œΏΘΚ
Θ®2Θ©»γΆΦ2Θ§»γΙϊ60ΓψΘΦΓœBACΘΦ90ΓψΘ§BDΘ§CDΖ÷±πΫΜΓ―O”ΎEΘ§FΘ§―–ΨΩΈε±Ώ–ΈABEFCΒΡ–‘÷ ΘΜ
ΔΌΧΫΥςAEΓΔAFΚΆBCΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘΚ
ΔΎ»γΆΦ3Θ§»τΓ―OΒΡΑκΨΕΈΣ4Θ§ΓœBACΘΫ75ΓψΘ§«σ±ΏEFΒΡ≥ΛΘΜ
Δέ»τABΘΫcΘ§ACΘΫbΘ§÷±Ϋ”–¥≥ωBEΘ§CFΒΡ ΐΝΩΙΊœΒΘ°
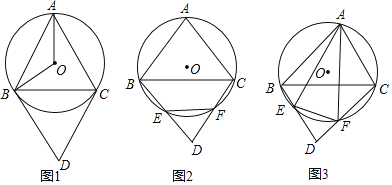
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©ΔΌAEΘΫBCΘ§AFΘΫBCΘ§άμ”…ΦϊΫβΈωΘΜΔΎEFΘΫ4ΘΜΔέ![]() ΘΫ
ΘΫ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©œκΑλΖ®÷ΛΟςOBΓΆBDΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©ΔΌΫα¬έΘΚAEΘΫBCΘ§AFΘΫBCΘ°œκΑλΖ®÷ΛΟςΜΓAB=ΜΓEC,ΜΓAE=ΜΓBCΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΔΎ»γΆΦ3÷–Θ§Ν§Ϋ”OEΘ§OFΘ§ECΘ§BFΘ°÷ΛΟςΓςOEF «Β»±Ώ»ΐΫ«–ΈΦ¥Ω…ΫβΨωΈ ΧβΘ°
Δέάϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΫβΨωΈ ΧβΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©»γΆΦ1÷–Θ§
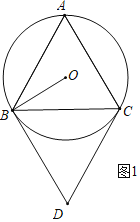
ÿBDøACȧCDøABȧ
ΓύΥΡ±Ώ–ΈABDC «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύABΘΫCDΘ§BDΘΫACΘ§
ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύABΘΫBCΘΫACΘ§
ΓύBCΘΫBDΘΫCDΘ§
ΓύΓςBCD «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœCBDΘΫ60ΓψΘ§
ΓΏΒψO «Β»±ΏΓςABCΒΡΆβ–ΡΘ§
ΓύΓœOCBΘΫ30ΓψΘ§
ΓύΓœOBDΘΫ90ΓψΘ§
ΓύOBΓΆBDΘ§
ΓύBD «Γ―OΒΡ«–œΏΘ°
Θ®2Θ©ΔΌΫα¬έΘΚAEΘΫBCΘ§AFΘΫBCΘ°
άμ”…ΘΚ»γΆΦ2÷–Θ§Ν§Ϋ”BFΘ§ECΘ°
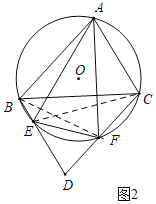
ÿBDøACȧ
ΓύΓœACBΘΫΓœCBEΘ§
ΓύΜΓAB=ΜΓEC,
ΓύΜΓAE=ΜΓBCΘ§
ΓύAEΘΫBCΘ§Ά§Ζ®Ω…÷ΛΘΚAFΘΫBCΘ°
ΔΎ»γΆΦ3÷–Θ§Ν§Ϋ”OEΘ§OFΘ§ECΘ§BFΘ°
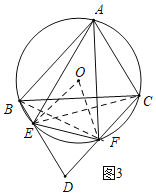
”…ΔΌΩ…÷ΣAEΘΫAFΘ§
ΓύΓœAEFΘΫΓœAFEΘ§
ΓΏΜΓAE=ΜΓBCΘ§
ΓύΓœACEΘΫΓœBACΘΫ75ΓψΘ§
ΓύΓœAFEΘΫΓœACEΘΫ75ΓψΘ§
ΓύΓœAEFΘΫΓœAFEΘΫ75ΓψΘ§
ΓύΓœEAFΘΫ180Γψ©¹75Γψ©¹75ΓψΘΫ30ΓψΘ§
ΓύΓœEOFΘΫ2ΓœEAFΘΫ60ΓψΘ§
ΓΏOEΘΫOFΘ§
ΓύΓςOEF «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύEFΘΫOEΘΫ4Θ°
ΔέΫα¬έΘΚ![]() Θ°
Θ°
άμ”…ΘΚ»γΆΦ3÷–Θ§ΓΏΓœEFD+ΓœEFC=180ΓψΘ§ΓœEFC+ΓœDBC=180ΓψΘ§
ΓύΓœEFD=ΓœDBCΘ§
ΓύΓςDFEΓΉΓςDBCΘ§
ΓύΓςDFEΓΉΓςDBCΘ§
Γύ![]() Θ§
Θ§
ΓΏΥΡ±Ώ–ΈABDC «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύAB=CD=cΘ§BD=AC=bΘ§
Γύ![]() Θ°
Θ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Β»―ϋ÷±Ϋ«![]() ΒΡΕΞΒψ
ΒΡΕΞΒψ![]() ‘Ύ’ΐΖΫ–Έ
‘Ύ’ΐΖΫ–Έ![]() ΒΡΕ‘Ϋ«œΏ
ΒΡΕ‘Ϋ«œΏ![]() …œΘ§
…œΘ§![]() Υυ‘ΎΒΡ÷±œΏΫΜ
Υυ‘ΎΒΡ÷±œΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§![]() . œ¬Ν–Ϋα¬έ÷–Θ§’ΐ»ΖΒΡ”–_________ Θ®Χν–ρΚ≈Θ©.
. œ¬Ν–Ϋα¬έ÷–Θ§’ΐ»ΖΒΡ”–_________ Θ®Χν–ρΚ≈Θ©.
ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() «
«![]() ΒΡ“ΜΗω»ΐΒ»Ζ÷ΒψΘΜΔέ
ΒΡ“ΜΗω»ΐΒ»Ζ÷ΒψΘΜΔέ![]() ΘΜΔή
ΘΜΔή![]() ΘΜΔί
ΘΜΔί![]() .
.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΈΣΓ―OΒΡ÷±ΨΕ Θ§ΒψC‘ΎΓ―O…œΘ§ΙΐΒψOΉς![]() ΫΜBC”ΎΒψEΘ§ΫΜΓ―O”ΎΒψDΘ§CDΓΈAB.
ΫΜBC”ΎΒψEΘ§ΫΜΓ―O”ΎΒψDΘ§CDΓΈAB.
(1)«σ÷ΛΘΚEΈΣODΒΡ÷–ΒψΘΜ
(2)»τCB=6Θ§«σΥΡ±Ώ–ΈCAODΒΡΟφΜΐ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®Έ Χβ«ιΨ≥Θ©
»γΆΦ1Θ§ΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§M «BC±Ώ…œΒΡ“ΜΒψΘ§E «CD±ΏΒΡ÷–ΒψΘ§AEΤΫΖ÷ΓœDAMΘ°
Θ®ΧΫΨΩ’Ι ΨΘ©
(1)÷ΛΟςΘΚAM=AD+MCΘΜ
(2)AM=DE+BM «Ζώ≥…ΝΔΘΩ»τ≥…ΝΔΘ§«κΗχ≥ω÷ΛΟςΘΜ»τ≤Μ≥…ΝΔΘ§«κΥΒΟςάμ”…Θ°
Θ®ΆΊ’Ι―”…λΘ©
(3)»τΥΡ±Ώ–ΈABCD «≥Λ”κΩμ≤ΜœύΒ»ΒΡΨΊ–ΈΘ§ΤδΥϊΧθΦΰ≤Μ±δΘ§»γΆΦ2Θ§ΧΫΨΩ’Ι Ψ(1)ΓΔ(2)÷–ΒΡΫα¬έ «Ζώ≥…ΝΔΘΩ«κΖ÷±πΉς≥ω≈–ΕœΘ§≤Μ–η“Σ÷ΛΟςΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
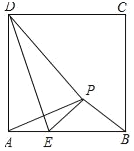
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ§ADΘΫ![]() +2Θ§“―÷ΣΒψE «±ΏAB…œΒΡ“ΜΕ·ΒψΘ®≤Μ”κAΓΔB÷ΊΚœΘ©ΫΪΓςADE―ΊDEΕ‘’έΘ§ΒψAΒΡΕ‘”ΠΒψΈΣPΘ§Β±ΓςAPB «Β»―ϋ»ΐΫ«–Έ ±Θ§AEΘΫ_____Θ°
+2Θ§“―÷ΣΒψE «±ΏAB…œΒΡ“ΜΕ·ΒψΘ®≤Μ”κAΓΔB÷ΊΚœΘ©ΫΪΓςADE―ΊDEΕ‘’έΘ§ΒψAΒΡΕ‘”ΠΒψΈΣPΘ§Β±ΓςAPB «Β»―ϋ»ΐΫ«–Έ ±Θ§AEΘΫ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΝΫΗωΑκΨΕœύΒ»ΒΡ÷±Ϋ«…»–ΈΒΡ‘≤–ΡΖ÷±π‘ΎΕ‘ΖΫΒΡ‘≤ΜΓ…œΘ§ΑκΨΕAEΓΔCFΫΜ”ΎΒψGΘ§ΑκΨΕBEΓΔCDΫΜ”ΎΒψHΘ§«“ΒψC «ΜΓABΒΡ÷–ΒψΘ§»τ…»–ΈΒΡΑκΨΕΈΣ![]() Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΒ»”Ύ_____Θ°
Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΒ»”Ύ_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣABCD.
Θ®1Θ©ΉςΓœBΒΡΤΫΖ÷œΏΫΜAD”ΎEΒψΓΘΘ®”Ο≥ΏΙφΉςΆΦΖ®Θ§±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ“Σ«σ–¥ΉςΖ®)ΘΜ
Θ®2Θ©»τABCDΒΡ÷ή≥ΛΈΣ10Θ§CD=2Θ§«σDEΒΡ≥ΛΓΘ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Βψ![]() ΒΡΉχ±ξΖ÷±πΈΣ
ΒΡΉχ±ξΖ÷±πΈΣ![]() ΚΆ
ΚΆ![]() Θ§≈ΉΈοœΏ
Θ§≈ΉΈοœΏ![]() ΒΡΕΞΒψ‘ΎœΏΕΈ
ΒΡΕΞΒψ‘ΎœΏΕΈ![]() …œ‘ΥΕ·Θ§”κ
…œ‘ΥΕ·Θ§”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΝΫΒψΘ®
ΝΫΒψΘ®![]() ‘Ύ
‘Ύ![]() ΒΡΉσ≤ύΘ©Θ§»τΒψ
ΒΡΉσ≤ύΘ©Θ§»τΒψ![]() ΒΡΚαΉχ±ξΒΡΉν–Γ÷ΒΈΣ0Θ§‘ρΒψ
ΒΡΚαΉχ±ξΒΡΉν–Γ÷ΒΈΣ0Θ§‘ρΒψ![]() ΒΡΚαΉχ±ξΉν¥σ÷ΒΈΣΘ® Θ©
ΒΡΚαΉχ±ξΉν¥σ÷ΒΈΣΘ® Θ©

A.6B.7C.8D.9
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
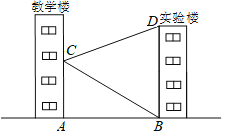
ΓΨΧβΡΩΓΩ»γΆΦΘ§―ß–ΘΫΧ―ß¬ΞΕ‘Οφ «“Μ¥± Β―ι¬ΞΘ§–Γ÷λ‘ΎΫΧ―ß¬ΞΒΡ¥ΑΩΎC≤βΒΟ Β―ι¬ΞΕΞ≤ΩDΒΡ―ωΫ«ΈΣ20ΓψΘ§ Β―ι¬ΞΒΉ≤ΩBΒΡΗ©Ϋ«ΈΣ30ΓψΘ§ΝΩΒΟΫΧ―ß¬Ξ”κ Β―ι¬Ξ÷°ΦδΒΡΨύάκABΘΫ30mΘ°«σ Β―ι¬ΞΒΡΗΏBDΘ°Θ®ΫαΙϊΨΪ»ΖΒΫ1mΘ°≤ΈΩΦ ΐΨίtan20ΓψΓ÷0.36Θ§sin20ΓψΓ÷0.34Θ§cos20ΓψΓ÷0.94Θ§![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com