
【题目】如图,AB为⊙O的直径 ,点C在⊙O上,过点O作![]() 交BC于点E,交⊙O于点D,CD∥AB.
交BC于点E,交⊙O于点D,CD∥AB.
(1)求证:E为OD的中点;
(2)若CB=6,求四边形CAOD的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由垂径定理得![]() ,由两直线平行,内错角相等,得
,由两直线平行,内错角相等,得![]() ,由角边角可证得
,由角边角可证得![]() 与
与![]() ,由全等三角形的对应边相等,即可得证;
,由全等三角形的对应边相等,即可得证;
(2)连接![]() ,由直径所对的圆周角是
,由直径所对的圆周角是![]() °,得
°,得![]() °,由垂径定理,得∴
°,由垂径定理,得∴![]() =
= ![]() ,
,
![]() ∥
∥![]() ,所以四边形
,所以四边形![]() 是平行四边形,由线段垂直平分线的性质可得
是平行四边形,由线段垂直平分线的性质可得![]() ,可证
,可证![]() 是等边三角形,
是等边三角形, ![]() °.在
°.在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
, ![]() .由此,
.由此, ![]() ,可得四边形CAOD的面积为
,可得四边形CAOD的面积为![]() .
.
试题解析:(1)∵在⊙O中, ![]() 于
于![]() ,
,
∴![]() ,
,
∵CD∥AB,
∴![]() .
.
在![]() 与
与![]() 中,
中, 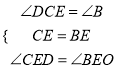 ,
,
∴![]() ≌
≌![]()
∴![]() ,
,
∴![]() 为
为![]() 的中点;
的中点;
(2)连接![]() ,
,
∵![]() 是⊙O的直径,
是⊙O的直径,
∴![]() °,
°,
∵![]() ,
,
∴![]() °=
°= ![]() ,
,
∴![]() ∥
∥![]() ,
,
∵![]() ∥
∥![]() ,
,
∴四边形![]() 是平行四边形
是平行四边形
∵![]() 是
是![]() 的中点,
的中点, ![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() °,
°,
∴![]() °
°![]() °,
°,
∴在![]() 中,
中, ![]() .
.
∵![]()
∴![]() .
.
∵![]() ,
,
∴![]() ,
, ![]() .
.
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在下列条件中,△ABC不是直角三角形的是 ( )
A. b2=a2-c2 B. ∠A:∠B:∠C=3:4:5
C. ∠C=∠A-∠B D. a2:b2:c2=1:3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30![]() ,CF=
,CF=![]() ,则DH=______.
,则DH=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( ).
① 相等的角是对顶角;② 同旁内角互补;③ 在同一平面内,若a//b,b//c,则a//c;④ 末位是零的整数能被5整除.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
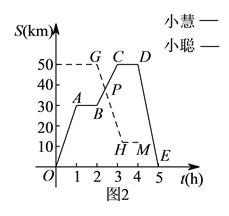
【题目】小聪和小慧在某风景区(如图![]() )沿景区公路游览,约好在宾馆见面.上午
)沿景区公路游览,约好在宾馆见面.上午![]() ,小慧乘坐车速为
,小慧乘坐车速为![]() 的电动汽车从宾馆出发,先后在两个景点游玩
的电动汽车从宾馆出发,先后在两个景点游玩![]() 分钟和
分钟和![]() 分钟后回到宾馆.小聪骑自行车从飞瀑出发,车速为
分钟后回到宾馆.小聪骑自行车从飞瀑出发,车速为![]() ,他先后在两个景点游玩了
,他先后在两个景点游玩了![]() 分钟和
分钟和![]() 分钟后回到宾馆.图
分钟后回到宾馆.图![]() 中的图象分别表示小慧和小聪离宾馆的路程
中的图象分别表示小慧和小聪离宾馆的路程![]() 与时间
与时间![]() 的函数关系(不全).试结合图中信息回答:
的函数关系(不全).试结合图中信息回答:
(![]() )小慧游览的景点是__________,点
)小慧游览的景点是__________,点![]() 的坐标为__________.
的坐标为__________.
(![]() )当小聪和小慧相遇时,叫他们距离宾馆多少千米?
)当小聪和小慧相遇时,叫他们距离宾馆多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com