
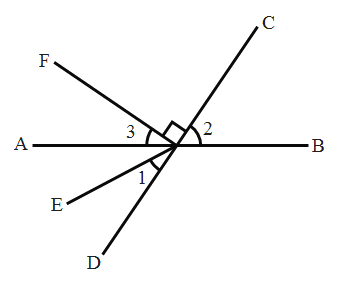
【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC .
(1)图中∠AOF的余角是_____________ (把符合条件的角都填上);
(2)如果∠1=28° ,求∠2和∠3的度数.
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
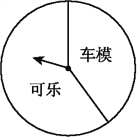
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于E,CF⊥BD于E,图中全等三角形有( )

A. 3对 B. 5对 C. 6对 D. 7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
2,﹣4,8,﹣16,32,﹣64,…
4,﹣2,10,﹣14,34,﹣62,…
﹣1,2,﹣4,8,﹣16,32,…
在上面三行数的第n列中,从上往下的三个数分别记为a,b,c,观察这些数的特点,根据你所得到的规律,解答下列为问题.
(1)用含n的式子分别表示出a,b,c;
(2)根据(1)的结论,若a,b,c三个数的和为770,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
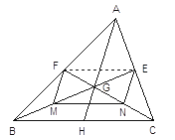
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B是数轴上原点O两侧的两点,其中点A在负半轴上,点B在正半轴上,AO=2, OB=10.动点P从点A出发以每秒2个单位长度的速度向右运动,到达点B后立即返回,速度不变;动点Q从点O出发以每秒1个单位长度的速度向右运动,当点Q到达点B时,动点P,Q停止运动.设P,Q两点同时出发,运动时间为t秒.
(1)当点P从点A向点B运动时,点P在数轴上对应的数为 当点P从点B返回向点O运动时,点P在数轴上对应的数为 (用含t的代数式表示)
(2)当t为何值时,点P,Q第一次重合?
(3)当t为何值时,点P,Q之间的距离为3个单位?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,对于
,对于![]() 的横长、纵长、纵横比给出如下定义:
的横长、纵长、纵横比给出如下定义:
将![]() 中的最大值,称为
中的最大值,称为![]() 的横长,记作
的横长,记作![]() ;将
;将![]() 中的最大值,称为
中的最大值,称为![]() 的纵长,记作
的纵长,记作![]() ;将
;将![]() 叫做
叫做![]() 的纵横比,记作
的纵横比,记作![]() .
.
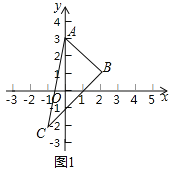
例如:如图![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,则
,则![]() ,
,
所以![]() .
.
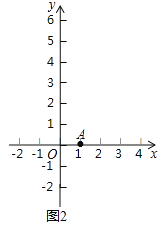
![]() 如图2,点
如图2,点![]() ,
,
![]() 点
点![]() ,
,
则![]() 的纵横比
的纵横比![]() ______
______
![]() 的纵横比
的纵横比![]() ______;
______;
![]() 点F在第四象限,若
点F在第四象限,若![]() 的纵横比为1,写出一个符合条件的点F的坐标;
的纵横比为1,写出一个符合条件的点F的坐标;
![]() 点M是双曲线
点M是双曲线![]() 上一个动点,若
上一个动点,若![]() 的纵横比为1,求点M的坐标;
的纵横比为1,求点M的坐标;
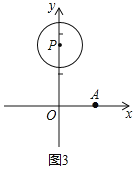
![]() 如图3,点
如图3,点![]() 以
以![]() 为圆心,1为半径,点N是
为圆心,1为半径,点N是![]() 上一个动点,直接写出
上一个动点,直接写出![]() 的纵横比
的纵横比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%.为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:㎡),绘制了统计图,如图所示,下面有四个推断:
① 年用水量不超过180㎡的该市居民家庭按第一档水价交费
② 年用水量超过240㎡的该市居民家庭按第三档水价交费
③ 该市居民家庭年用水量的中位数在150-180之间
④ 该市居民家庭年用水量的平均数不超过180
正确的是( )
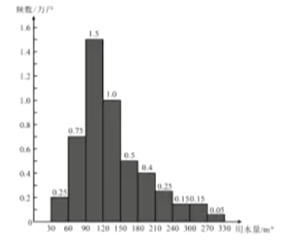
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)在图1中,∠AOC= °,∠MOC= °;
(2)将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;
(3)将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com