
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.
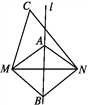
∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为 . 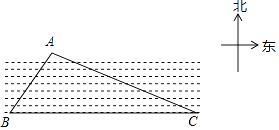
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一条直线上从左往右依次有A、B、C、D四个点.
![]()
(1)如果线段AC、BC、BD的长分别为3a-b、a+b、4a-2b,试求A、D两点间的距离;
(2)如果将这条直线看作是以点C为原点的数轴(向右为正方向).
①直接写出数轴上与点B距离为a+2b的点所表示的数______;
②设线段BD上一动点P所表示的数为x,求|x+a+b|+|x-3a+3b|的值(用含a、b的代数表示);
③线段BD上有两个动点P、M,点P所表示的数为x,点M所表示的数为y,直接写出式子|x-y|+|x+a+b|+|x-y-6a+4b|的最小值______(用含a、b的代数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年1月份的月历表中,任意框出表中竖列上三个相邻的数(如图,如框出了10,17,24),则这三个数的和可能的是( )

A. 21B. 27C. 50D. 75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
(1)在这个问题中,自变量是什么?因变量是什么?
(2)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(3)第三天12时这头骆驼的体温是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于![]() MN的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2,正确的序号是_____.
MN的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2,正确的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A,B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.
(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com