
【题目】一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是![]() .
.
(1)铅球行进的最大高度是多少?
(2)该男生把铅球推出的水平距离是多少?
(3)铅球在下落的过程中,行进高度由![]() m变为
m变为![]() m时,铅球行进的水平距离是多少?
m时,铅球行进的水平距离是多少?
【答案】(1)3m;(2)4m.
【解析】试题分析:(1)通过配方法把函数的解析式化为顶点式,然后跟据抛物线的性质可求其最值;
(2)令y=0,求出落地点,得到铅球被推出的水平距离;
(3)利用代入法分别求出横坐标的值,求出铅球行进的水平距离.
试题解析:(1) ![]() =
=![]()
∵![]() ,y的最大值为3,即铅球行进的最大高度是3m.
,y的最大值为3,即铅球行进的最大高度是3m.
(2)由y=0得, ![]()
解这个方程得,x1=10,x2=-2(负值舍去).
∴该男生把铅球推出的水平距离是10 m.
(3) 由函数![]() 的性质及上问可知,铅球下落过程中4≤x<10.
的性质及上问可知,铅球下落过程中4≤x<10.
由![]() ,解得x1=3(舍去),x2=5.
,解得x1=3(舍去),x2=5.
由![]() ,解得x1=-1(舍去),x2=9.
,解得x1=-1(舍去),x2=9.
9-5=4,
∴铅球行进的水平距离是4m.


科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,以点
是菱形,以点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系.若点
轴建立平面直角坐标系.若点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() .
.
(1)求菱形![]() 的边长;
的边长;
(2)证明![]() 为直角三角形;
为直角三角形;
(3)直线![]() 上是否存在一点
上是否存在一点![]() 使得
使得![]() 的面积与
的面积与![]() 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某百货商店服装柜在销售中发现:某品牌童装每天可售出20件,每件盈利40元,经市场调查发现,在进货价不变的情况下,若每件童装每降价1元,日销售量将增加2件.
(1)当每件童装降价多少元时,一天的盈利最多?
(2)若商场要求一天的盈利为1200元,同时又使顾客得到实惠,每件童装降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数图象经过(﹣2,4).
(1)如果点(a,1)和(﹣1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q,S△OPQ=![]() ,求Q的坐标.
,求Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
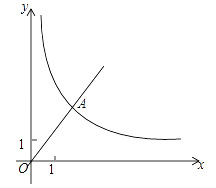
【题目】已知:如图,在平面直角坐标系中,正比例函数y=![]() 的图象经过A,点A的纵坐标为4,反比例函数y=
的图象经过A,点A的纵坐标为4,反比例函数y=![]() 的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
(1)这个反比例函数的解析式;
(2)ΔABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;
②AD与AC互相垂直;
③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;
⑤线段AB是B点到AC的距离.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣4)2007·(0.25)2018
(2)3(2﹣y)2﹣4(y+5)
(3)(a+2b)(a﹣2b)﹣![]() b(a﹣8b)
b(a﹣8b)
(4)(a﹣b)(a2+ab+b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com