练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

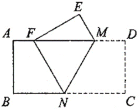
    【题目】如图，矩形ABCD中，点M、N分别在AD、BC边上，将矩形ABCD沿MN翻折，点C恰好落在AD边上的点F处，若MD=1，∠MNC=60°，则AB的长为_____.

    【答案】

    【解析】

    由翻折变换可得EF＝CD，MD＝EM＝1，∠MNC＝∠FNM＝60°，∠C＝∠EFN＝90°，由平行线的性质可得∠FMN＝∠MNC＝60°，即可求∠EFM＝30°，由直角三角形的性质可求解．

    解：∵将矩形ABCD沿MN翻折，点C恰好落在AD边上的点F处．

    ∴EF＝CD，MD＝EM＝1，∠MNC＝∠FNM＝60°，∠C＝∠EFN＝90°

    ∵AD∥BC，

    ∴∠FMN＝∠MNC＝60°，

    ∴∠MFN＝60°，

    ∴∠EFM＝30°，且∠E＝90°，

    ∴EF＝EM＝，

    ∴AB＝CD＝，

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义一种对正整数n的“F”运算：①当n为奇数时，F（n）=3n+1；②当n为偶数时，F（n）=（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n=24，则：

    若n=13，则第2018次“F”运算的结果是（　　）

    A. 1 B. 4 C. 2018 D. 42018

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．

    （1）若从中任取一个球，球上的汉字刚好是“福”的概率为多少？

    （2）小颖从中任取一球，记下汉字后放回袋中，然后再从中任取一球，求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC=3∠2，③∠BOC=90°+∠1，④∠BOC=90°+∠2正确的是（　　）

    A. ①②③ B. ①③④ C. ①④ D. ①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的，如果规定向东为正，向西为负，他这天上午的行程是（单位：千米）：＋15，－3，＋16，－11，＋10，－12，＋4，－15，＋16，－18．

    （1）将最后一名乘客送达目的地时，小张距上午出发点的距离是多少千米？在出发点的什么方向？

    （2）若汽车耗油量为0．6升/千米，出车时，邮箱有油72．2升，若小张将最后一名乘客送达目的地，再返回出发地，问小张今天上午是否需要加油？若要加油至少需要加多少才能返回出发地？若不用加油，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【操作发现】

    如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．

    （1）请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；

    （2）在（1）所画图形中，∠AB′B=　 　．

    【问题解决】

    如图②，在等边三角形ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．

    小明同学通过观察、分析、思考，对上述问题形成了如下想法：

    想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；

    想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．

    …

    请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）

    【灵活运用】

    如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），求BD的长（用含k的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件．投入市场后，游戏软件的利润占这4款软件总利润的40%．如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图．

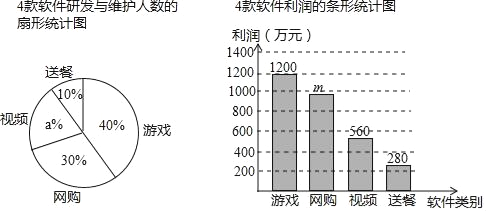
    根据以上信息，网答下列问题

    （1）直接写出图中a，m的值；

    （2）分别求网购与视频软件的人均利润；

    （3）在总人数和各款软件人均利润都保持不变的情况下，能否只调整网购与视频软件的研发与维护人数，使总利润增加60万元？如果能，写出调整方案；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则=____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

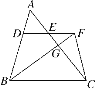
    【题目】已知如图，D是△ABC的边AB上一点，DE∥BC，交边AC于点E，延长DE至点F，使EF＝DE，连接BF，交边AC于点G，连接CF.

    (1)求证：；

    (2)如果CF2＝FG·FB，求证：CG·CE＝BC·DE.

    查看答案和解析>>

    同步练习册答案