
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限内交于A,B两点,点A的纵坐标为4,点B的坐标为(3,2),连接0A,OB.
的图象在第一象限内交于A,B两点,点A的纵坐标为4,点B的坐标为(3,2),连接0A,OB.
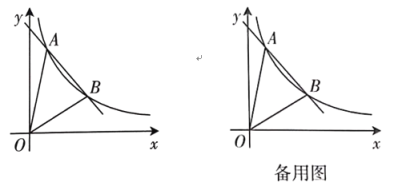
(1)求反比例函数的解析式;
(2)点M是线段AB上的一动点(不与点A,B重合),过点M作ME![]() x轴于点E,作MN
x轴于点E,作MN![]() y轴为于点N,求四边形MEON 的最大面积;
y轴为于点N,求四边形MEON 的最大面积;
(3)将直线y=kx+b向下平移n个单位长度,若直线与反比例函数在第一象限内的图象只有一个交点,求n的值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,四边形
时,四边形![]() 的面积最大,最大面积为
的面积最大,最大面积为![]() ;(3)
;(3)![]() .
.
【解析】
(1)把点![]() 代入反比例函数即可求解;
代入反比例函数即可求解;
(2)先求出直线AB的解析式为![]() ,设点M的坐标为
,设点M的坐标为![]() ,得到
,得到![]() ,
,![]() ,则
,则![]() ,根据二次函数的性质即可求出最大面积;
,根据二次函数的性质即可求出最大面积;
(3)设向下平移![]() 个单位长度后函数的解析式为
个单位长度后函数的解析式为![]() ,联立反比例函数得到一元二次方程,根据根的判别式即可求解.
,联立反比例函数得到一元二次方程,根据根的判别式即可求解.
(1)点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() .
.
∴反比例函数的解析式为![]() .
.
(2)∵点![]() 的纵坐标为4,
的纵坐标为4,
∴![]() ,
,
设直线![]() 的解析式为y=kx+b(k≠0)
的解析式为y=kx+b(k≠0)
把![]() 、
、![]() 代入得
代入得
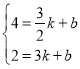 ,解得
,解得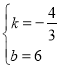
∴直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 为线段
为线段![]() 上的一动点,
上的一动点,
∴设点M的坐标为![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴当![]() 时,四边形
时,四边形![]() 的面积最大,最大面积为
的面积最大,最大面积为![]() .
.
(3)∵![]() ,
,
∴设向下平移![]() 个单位长度后函数的解析式为
个单位长度后函数的解析式为![]() .
.
令![]() ,整理,得
,整理,得![]() .
.
∵一次函数与反比例函数的图象在第一象限只有一个交点,
∴![]() 有唯一的实数根.
有唯一的实数根.
∴![]() .
.
∴![]() .
.
由题意得交点在第一象限内,
∴![]() 不符合题意,舍去.
不符合题意,舍去.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD 的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1CC1B1,延长C1B1交x轴于点A2,作正方形A2C1C2B2,…,按照这样的规律作正方形,则点B2019的纵坐标为_______.
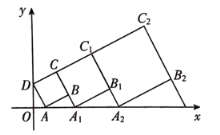
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佛山一环高速化改造后正式收费,车辆经过平胜大桥收费站时,设置了 4 个 ETC 智能收费(即不 需要人工收费)通道,分别为 A、B、C、D 通道,车辆可随机选择其中的一个直接读卡通过.
(1)一辆车经过此收费站时,选择 A 通道通过的概率是___________;
(2)现有甲、乙两辆小车从同一方向通过此收费站,请你用树状图或列表格求出两辆车选择不同通道通过的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
(一)猜测探究
在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.
(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是_______,NB与MC的数量关系是_______;
(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由。
(二)拓展应用
如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=90°,∠C1=30°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旅转60°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com