
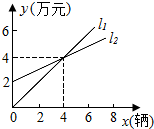
 如图,l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系;l2表示该电动车厂一天的销售成本与销售量的关系.
如图,l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系;l2表示该电动车厂一天的销售成本与销售量的关系.分析 (1)设y=kx,根据题意可知当x=4时,y=4,则k=1,即销售收入与销售量之间的函数关系式为y=x;
(2)设y=kx+b,把已知坐标代入可得解析式y=x+2;
(3)由图可知当x=4时,销售收入等于销售成本,故x=4;
解答 解:(1)设y=kx,
∵直线过(4,4)两点,
∴4=4k,
∴k=1,
∴y=x;
(2)设y=kx+b,
∵直线过(0,2)、(4,4)两点,
∴2=b,4=4k+2,
∴k=$\frac{1}{2}$,
∴y=$\frac{1}{2}$x+2;
(3)由图象知,当x=4时,销售收入等于销售成本,
∴x=$\frac{1}{2}$x+2,
∴x=4,
答:当一天的销售量为4辆时,销售收入等于销售成本.
点评 本题考查了考查了一次函数的应用,一次函数的图象和性质,正确理解题意看清图象是解题的关键.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)-3与23 | B. | (-2)-2与2-2 | C. | -33与(-$\frac{1}{3}$)3 | D. | (-3)-3与($\frac{1}{3}$)3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.
在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com