
分析 根据点E在直线AB上,AB=$\frac{3}{2}$AE,可得点E在BA延长线上或线段AB上,据此分两种情况进行讨论,根据等腰三角形的性质以及含30°角的直角三角形,求得CD的长即可.
解答 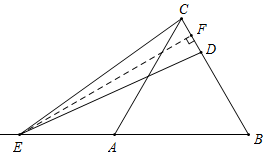 解:分两种情况:
解:分两种情况:
①当点E在BA延长线上时,过点E作EF⊥BC于F,则
Rt△BEF中,∠BEF=30°,
∵AB=$\frac{3}{2}$AE=6,
∴AE=4,
∴BF=$\frac{1}{2}$BE=$\frac{1}{2}$(4+6)=5,
∵BC=6,
∴CF=6-5=1,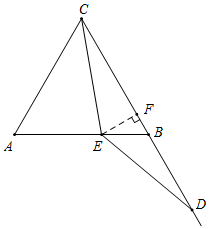
∵ED=EC,EF⊥CD,
∴CD=2CF=2;
②当点E在线段AB上时,过E作EF⊥BC于F,则
Rt△BEF中,∠BEF=30°,
∴BF=$\frac{1}{2}$BE=$\frac{1}{2}$(AB-AE)=1,
∵BC=6,
∴CF=6-1=5,
∵ED=EC,EF⊥CD,
∴CD=2CF=10.
综上所述,CD的长为2或10.
故答案为:2或10.
点评 本题主要考查了等边三角形的性质,等腰三角形的性质以及含30°角的直角三角形的性质,解决问题的关键是作辅助线构造直角三角形,依据等腰三角形的三线合一的性质进行计算.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
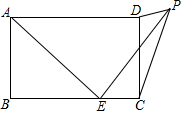 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-4,-6) | B. | (-4,-3) | C. | (-5,-2) | D. | (-5,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-4) | B. | (-2,-3) | C. | (-2,-2) | D. | (-2,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com