
分析 分为两种情况:①当圆心在三角形的内部时,②当圆心在三角形的外部时从圆心向BC引垂线,交点为D,则根据垂径定理和勾股定理可求出OD的长,即可求出高AD.
解答 解:分为两种情况:①如图1,当圆心在三角形的内部时,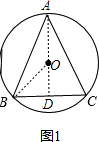
连接AO并延长交BC于D点,连接OB,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
根据垂径定理得AD⊥BC,
则BD=4,
在Rt△ODB中,由勾股定理得:OB2=OD2+BD2,
∵OB=5,BD=4,
∴OD=3,
∴高AD=5+3=8;
②当圆心在三角形的外部时,如图2,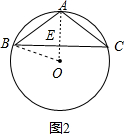
三角形底边BC上的高AD=5-3=2.
所以BC边上的高是8或2,
故答案为:8或2.
点评 本题综合考查了垂径定理和勾股定理在圆中的应用,因三角形与圆心的位置不明确,注意分情况讨论.


科目:初中数学 来源: 题型:选择题
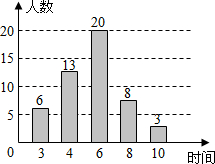 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
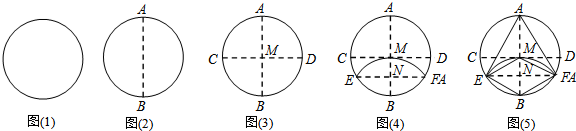
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
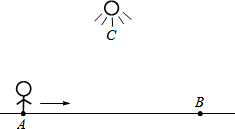 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )| A. | y=x? | B. | y=x+3 | C. | y=$\frac{3}{x}$? | D. | y=(x-3)2+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com