
【题目】如图1,四边形ABCD是正方形,点E是AB边的中点,以AE为边作正方形AEFG,连接DE,BG.
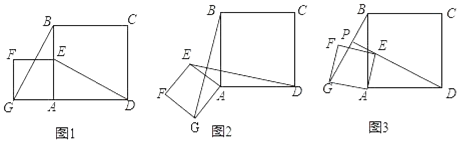
(1)发现
①线段DE、BG之间的数量关系是 ;
②直线DE、BG之间的位置关系是 .
(2)探究
如图2,将正方形AEFG绕点A逆时针旋转,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)应用
如图3,将正方形AEFG绕点A逆时针旋转一周,记直线DE与BG的交点为P,若AB=4,请直接写出点P到CD所在直线距离的最大值和最小值.
【答案】(1)发现:①DE=BG;②DE⊥BG;(2)探究:(1)中的结论仍然成立,理由详见解析;(3)应用:点P到CD所在直线距离的最大值是2+2![]() ,最小值是3﹣
,最小值是3﹣![]() .
.
【解析】
(1)证明△AED≌△AGB可得出两个结论;
(2)①根据正方形的性质得出AE=AG,AD=AB,∠EAG=∠DAB=90°,求出∠EAD=∠GAB,根据SAS推出△EAD≌△GAB即可;
②根据全等三角形的性质得出∠GBA=∠EDA,求出∠DHB=90°即可;
(3)先确定点P到CD所在直线距离的最大值和最小值的位置,再根据图形求解.
解:(1)①线段DE、BG之间的数量关系是:DE=BG,
理由是:如图1,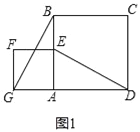
∵四边形ABCD是正方形,
∴AB=AD,∠BDA=90°,
∴∠BAG=∠BAD=90°,
∵四边形AEFG是正方形,
∴AE=AG,
∴△AED≌△AGB(SAS),
∴DE=BG;
②直线DE、BG之间的位置关系是:DE⊥BG,
理由是:如图2,延长DE交BG于Q,
由△AED≌△AGB得:∠ABG=∠ADE,
∵∠AED+∠ADE=90°,∠AED=∠BEQ,
∴∠BEQ+∠ABG=90°,
∴∠BQE=90°,
∴DE⊥BG;
故答案为:①DE=BG;②DE⊥BG;
(2)(1)中的结论仍然成立,理由是:
①如图3,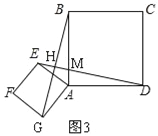
∵四边形AEFG和四边形ABCD是正方形,
∴AE=AG,AD=AB,∠EAG=∠DAB=90°,
∴∠EAD=∠GAB=90°+∠EAB,
在△EAD和△GAB中,
 ,
,
∴△EAD≌△GAB(SAS),
∴ED=GB;
②ED⊥GB,
理由是:∵△EAD≌△GAB,
∴∠GBA=∠EDA,
∵∠AMD+∠ADM=90°,∠BMH=∠AMD,
∴∠BMH+∠GBA=90°,
∴∠DHB=180°﹣90°=90°,
∴ED⊥GB;
(3)将正方形AEFG绕点A逆时针旋转一周,即点E和G在以A为圆心,以2为半径的圆上,过P作PH⊥CD于H,
①当P与F重合时,此时PH最小,如图4,
在Rt△AED中,AD=4,AE=2,
∴∠ADE=30°,DE=![]() =2
=2![]() ,
,
∴DF=DE﹣EF=2![]() ﹣2,
﹣2,
∵AD⊥CD,PH⊥CD,
∴AD∥PH,
∴∠DPH=∠ADE=30°,
∵cos30°=![]() =
=![]() ,
,
∴PH=![]() (2
(2![]() ﹣2)=3﹣
﹣2)=3﹣![]() ;
;
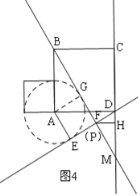
②∵DE⊥BG,∠BAD=90°,
∴以BD的中点O为圆心,以BD为直径作圆,P、A在圆上,
当P在![]() 的中点时,如图5,此时PH的值最大,
的中点时,如图5,此时PH的值最大,
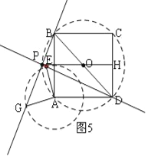
∵AB=AD=4,
由勾股定理得:BD=4![]() ,
,
则半径OB=OP=2![]() ,
,
∴PH=2+2![]() .
.
综上所述,点P到CD所在直线距离的最大值是2+2![]() ,最小值是3﹣
,最小值是3﹣![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
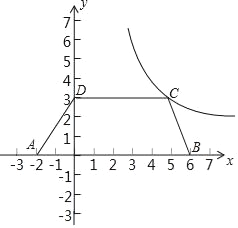
【题目】如图,在四边形ABCD中,CD∥AB,AD=BC.已知A(﹣2,0),B(6,0),D(0,3),函数y=![]() (x>0)的图象G经过点C.
(x>0)的图象G经过点C.
(1)求点C的坐标和函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)将四边形ABCD向上平移2个单位得到四边形A'B'C'D',问点B'是否落在图象G上?
查看答案和解析>>
科目:初中数学 来源: 题型:
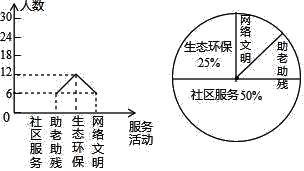
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(2,y2),C(3,y3),则y1、y2、y3的大小关系是( )
A. y1>y2>y3 B. y1>y3>y2 C. y2>y1>y3 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
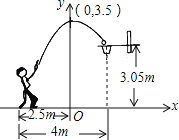
A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段路基的横断面是直角梯形,如图1,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图2的技术要求.试求出改造后坡面的坡度是多少?
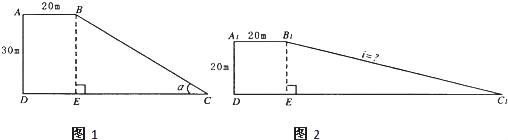
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com