
分析 (1)根据方程有两个实数根可以得到△≥0,从而求得k的取值范围;
(2)利用根与系数的关系将两根之和和两根之积代入代数式求k的值即可.
解答 解:(1)由题意得△=2-4k2=-8k+4≥0,
∴k≤$\frac{1}{2}$;
(2)由韦达定理得,x1+x2=2(k-1),x1x2=k2,
∴x12+x22=(x1+x2)2-2x1x2=2-2k2=14,
解得k=-1或5(5>$\frac{1}{2}$,舍去),
∴k=-1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
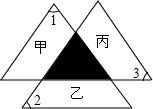 如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )
如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )| A. | 乙>甲>丙 | B. | 乙>丙>甲 | C. | 丙>甲>乙 | D. | 丙>乙>甲 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.
尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com