
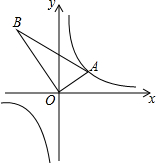
 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 要求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.根据条件得到△ACO∽△ODB,得到:$\frac{BD}{OC}$=$\frac{OD}{AC}$=$\frac{OB}{OA}$=2,然后用待定系数法即可.
解答 解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D,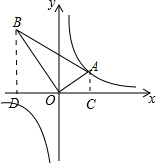
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA,
∴$\frac{BD}{OC}$=$\frac{OD}{AC}$=$\frac{OB}{OA}$,
∵OB=2OA,
∴BD=2m,OD=2n,
因为点A在反比例函数y=$\frac{1}{x}$的图象上,则mn=1,
∵点B在反比例函数y=$\frac{k}{x}$的图象上,B点的坐标是(-2n,2m),
∴k=-2n•2m=-4mn=-4.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,相似三角形的判定和性质,求函数的解析式的问题,一般要转化为求点的坐标的问题,求出图象上点的横纵坐标的积就可以求出反比例函数的解析式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
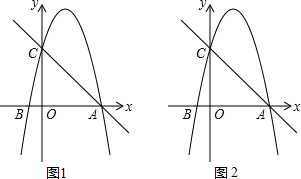
 如图,已知抛物线y=ax2+bx+3经过点B(-1,0)、C(3,0),交y轴于点A,
如图,已知抛物线y=ax2+bx+3经过点B(-1,0)、C(3,0),交y轴于点A,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明想测量院子里一棵树的高度,在某一时刻,他站在该树的影子上,前后移动,直到他本身的影子的顶端正好与树影的顶端重叠.此时,他与该树的水平距离2m,小明身高1.5m,他的影长是1.2m,那么该树的高度为4m.
如图,小明想测量院子里一棵树的高度,在某一时刻,他站在该树的影子上,前后移动,直到他本身的影子的顶端正好与树影的顶端重叠.此时,他与该树的水平距离2m,小明身高1.5m,他的影长是1.2m,那么该树的高度为4m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com