
【题目】如图,![]() 内接于
内接于![]() ,
,![]() ,BC与直径AD交于点E.
,BC与直径AD交于点E.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,在BC上取点G,使![]() ,连接AG并延长交
,连接AG并延长交![]() 于点F,求证:AF平分
于点F,求证:AF平分![]() ;
;
(3)如图3,在(2)的条件下,![]() ,求线段EG的长.
,求线段EG的长.

科目:初中数学 来源: 题型:
【题目】 如图,在△ABC中,∠ACB=90°,AC=BC过点C的射线CF交边AB于点F,AD⊥CF于点D,BE⊥CF于点E,AD=3,BE=1.
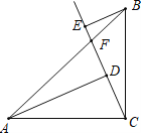
(1)求证:△ADC≌△CEB.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:平面内,如果一个四边形的四个顶点到某一点的距离都相等,则称这一点为该四边形的外心.
(1)下列四边形:平行四边形、矩形、菱形中,一定有外心的是 ;
(2)已知四边形ABCD有外心O,且A,B,C三点的位置如图1所示,请用尺规确定该四边形的外心,并画出一个满足条件的四边形ABCD;
(3)如图2,已知四边形ABCD有外心O,且BC=8,sin∠BDC=![]() ,求OC的长.
,求OC的长.
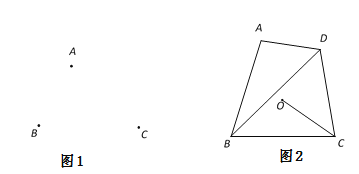
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:将矩形纸片ABCD折叠,使点A与点C重合(点D与D'为对应点),折痕为EF,连接AF.
(1)如图1,求证:四边形AECF为菱形;
(2)如图2,若FC=2DF,连接AC交EF于点O,连接DO、D'O,在不添加任何辅助线的情况下,请直接写出图2中所有等边三角形.
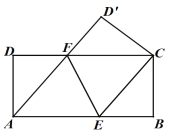

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的数学竞赛中,八(1)班比赛成绩分为![]() 、
、![]() 、
、![]() 、
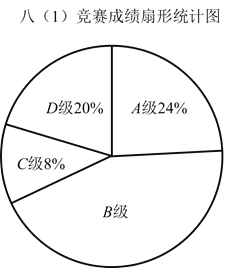
、![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩现整理并绘制成如下的统计图.请你根据以上提供的信息解答下列问题:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩现整理并绘制成如下的统计图.请你根据以上提供的信息解答下列问题:
(1)请补全条形统计图
(2)八年级一班竞赛成绩众数是________,中位数落在________类.
(3)若该校有1500名学生,请估计该校本次竞赛成绩为![]() 类的学生人数.
类的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某宾馆大厅要铺圆环形的地毯,工人师傅只测量了与小圆相切的大圆的弦AB的长,就计算出了圆环的面积,若测量得AB的长为20米,则圆环的面积为( )
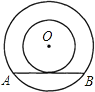
A. 10平方米B. 10π平方米C. 100平方米D. 100π平方米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com