
【题目】如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线y=x上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
A.(22014 , 22014)
B.(22015 , 22015)
C.(22014 , 22015)
D.(22015 , 22014)
【答案】A
【解析】解:∵OA1=1,
∴点A1的坐标为(1,0),
∵△OA1B1是等腰直角三角形,
∴A1B1=1,
∴B1(1,1),
∵△B1A1A2是等腰直角三角形,
∴A1A2=1,B1A2=![]() ,
,
∵△B2B1A2为等腰直角三角形,
∴A2A3=2,
∴B2(2,2),
同理可得,B3(22 , 22),B4(23 , 23),…Bn(2n﹣1 , 2n﹣1),
∴点B2015的坐标是(22014 , 22014).
故选:A.
根据OA1=1,可得点A1的坐标为(1,0),然后根据△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,求出A1A2 , B1A2 , A2A3 , B2A3…的长度,然后找出规律,求出点B2015的坐标.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.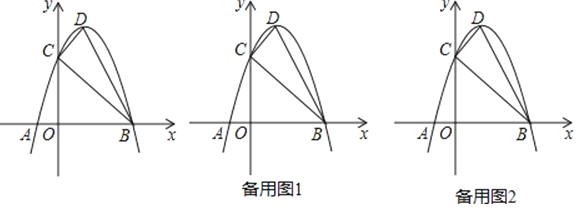
(1)填空:点C的坐标为 点D的坐标为 ;
(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点E,F分别是边AB,AC的中点,点D在边BC上.若DE=DF,AD=2,BC=6,求四边形AEDF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.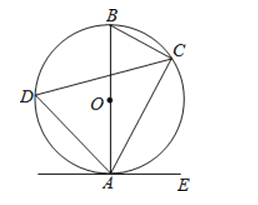
(1)求证:直线AE是⊙O的切线
(2)若∠D=60°,AB=6时,求劣弧![]() 的长(结果保留π)
的长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进杨梅的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则 cos∠MCN= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: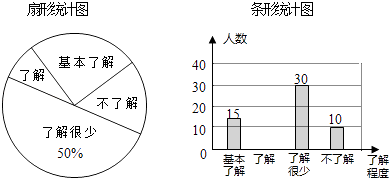
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com