
【题目】(1)如图1,在△ABC中,AD、BD分别平分∠BAC和∠ABC,AD、BD相交于点D,过点D作DE∥AC,DF∥BC分别交AB于点E、F.
①若∠EDF=80°,则∠ADB=________°;
②若∠C=![]() 则∠ADB=________°.
则∠ADB=________°.
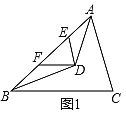
(2)如图2,在△ABC中,若∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,AD、BD相交于点D,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=60°,则∠ADB=_______°;
∠ABC,AD、BD相交于点D,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=60°,则∠ADB=_______°;
(3)如图3,在△ABC中,AD、BD分别是∠BAC、∠ABC的![]() 等分线,AD、BD相交于点D,若∠BAD=
等分线,AD、BD相交于点D,若∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=
∠ABC,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=![]() ,则∠ADB的度数是多少?(用
,则∠ADB的度数是多少?(用![]() 表示)
表示)
【答案】(1)130°、(90-0.5x)(2)140°;(3)![]()
【解析】
(1)①由∠EDF=80°及DE∥AC,DF∥BC,可求∠BAC+∠ABC =100°;再结合角平分线的定义及三角形的内角和即可求出∠ADB的值;②由角平分线的定义及三角形的内角和求解即可;
(2)参考(1)①的步骤求解即可;
(3)参考(2)的步骤求解即可.
(1)①∵∠EDF=80°,
∴∠DEF+∠DFE=100°.
∵DE∥AC,DF∥BC,
∴∠BAC=∠DEF,∠ABC=∠DFE,
∴∠BAC+∠ABC =100°.
∵AD、BD分别平分∠BAC和∠ABC,
∴∠BAD=![]() ∠BAC, ∠ABD=
∠BAC, ∠ABD=![]() ∠ABC,
∠ABC,
∴∠BAD+∠ABD=![]() (∠BAC+∠ABC)=50°,
(∠BAC+∠ABC)=50°,
∴∠ADC=180°-50°=130°;
②∵∠C=![]() ,
,
∴∠BAC+∠ABC =180°-![]() ,
,
∵AD、BD分别平分∠BAC和∠ABC,
∴∠BAD=![]() ∠BAC, ∠ABD=
∠BAC, ∠ABD=![]() ∠ABC,
∠ABC,
∴∠BAD+∠ABD=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (∠180°-
(∠180°-![]() )=(90-0.5x)°;
)=(90-0.5x)°;
(2)∵∠EDF=60°,
∴∠DEF+∠DFE=120°.
∵DE∥AC,DF∥BC,
∴∠BAC=∠DEF,∠ABC=∠DFE,
∴∠BAC+∠ABC =120°.
∵∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,
∠ABC,
∴∠BAD+∠ABD=![]() (∠BAC+∠ABC)=40°,
(∠BAC+∠ABC)=40°,
∴∠ADC=180°-40°=140°;
(3)∵∠EDF=![]() ,
,
∴∠DEF+∠DFE=120°.
∵DE∥AC,DF∥BC,
∴∠BAC=∠DEF,∠ABC=∠DFE,
∴∠BAC+∠ABC =(180-x)°.
∵BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,
∠ABC,
∴∠BAD+∠ABD=![]() (180-x)°,
(180-x)°,
∴∠ADC=180°-![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() 的对称轴为
的对称轴为 ![]() ,交
,交 ![]() 轴的一个交点为(
轴的一个交点为( ![]() ,0),且
,0),且 ![]() , 则下列结论:①
, 则下列结论:① ![]() ,
, ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() . 其中正确的命题有( )个.
. 其中正确的命题有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下题和解题过程:化简![]() ,使结果不含绝对值.
,使结果不含绝对值.
解:当![]() 时,即
时,即![]() 时,
时,
原式![]()
![]() ;
;
当![]() ,即
,即![]() 时,
时,
原式![]()
![]()
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:![]() ;
;
(2)试探究:当![]() 分别为何值时,方程
分别为何值时,方程![]()
①无解,②只有一个解,③有两个解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD的平分线AE与∠BCD的平分线CE交于点E,若∠B=38°,∠D=20°,则∠AEC的度数为
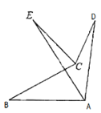
A. 9°B. 18°C. 22°D. 29°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:长方形ABCD中,点E为BC边的中点,将D折起,使点D落在点E处.

(1)请你用尺规作图画出折痕和折叠后的图形.(不要求写已知,求作和作法,保留作图痕迹)
(2)若折痕与AD、BC分别交于点M、N,与DE交于点O,求证△MDO≌△NEO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线 ![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥ ![]() 于点D.
于点D.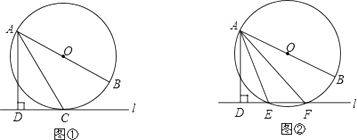
(1)如图①,当直线 ![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线 ![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: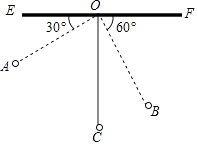
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com