
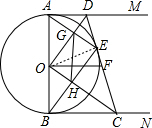
 如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.
如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
| 1 |
| 2 |
| 24 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OD2+OC2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6×8 |
| 10 |
| 24 |
| 5 |
| 48 |
| 5 |
| 1 |
| 2 |
| 24 |
| 5 |


科目:初中数学 来源: 题型:
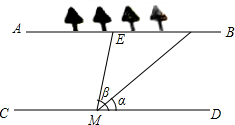 小明所在小组要测量护城河的宽度,如图所示是护城河的一段,AB、CD是两岸(两岸平行),河岸AB上有一排树,相邻两棵树之间的距离均为10米(树粗忽略不计).小明用测角仪在河岸CD的M处观测右数第一、四两棵树,观测线与CD所夹锐角分别为α、β.请你根据这些数据帮小明他们算出河宽(结果用含α、β的式子表示).
小明所在小组要测量护城河的宽度,如图所示是护城河的一段,AB、CD是两岸(两岸平行),河岸AB上有一排树,相邻两棵树之间的距离均为10米(树粗忽略不计).小明用测角仪在河岸CD的M处观测右数第一、四两棵树,观测线与CD所夹锐角分别为α、β.请你根据这些数据帮小明他们算出河宽(结果用含α、β的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:
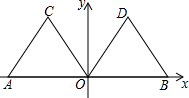 如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称都可以得到△OBD.
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称都可以得到△OBD.查看答案和解析>>
科目:初中数学 来源: 题型:
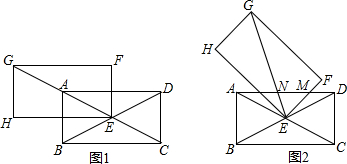
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com