
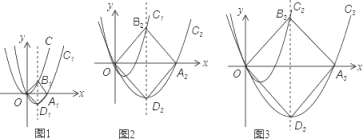
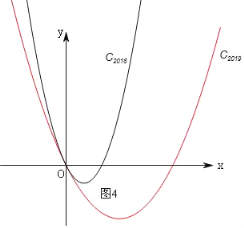
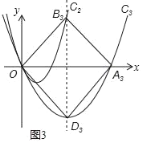
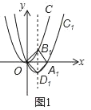
【题目】如图1,抛物线C:y=x2经过变换可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交于点A,且其对称轴分别交抛物线C、C1于点B1、D1.此时四边形OB1A1D1恰为正方形:按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交于点A2,且其对称轴分别交抛物线C1、C2于点B2、D2.此时四边形OB2A2D2也恰为正方形:按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3,请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线n:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1)
①请用含n的代数式直接表示出n的解析式;
②当x取任意不为0的实数时,试比较y2018与y2019的函数值的大小关系,并说明理由.
【答案】(1)1,2;(2)y2=![]() x2﹣2x,y3=
x2﹣2x,y3=![]() x2﹣2x;(3)①yn=
x2﹣2x;(3)①yn=![]() x2﹣2x(n≥1),②当x≠0时,y2018>y2019.
x2﹣2x(n≥1),②当x≠0时,y2018>y2019.
【解析】
(1)求与x轴交点A1坐标,根据正方形对角线性质表示出B1的坐标,代入对应的解析式即可求出对应的b1的值,写出D1的坐标,代入y1的解析式中可求得a1的值;
(2)求与x轴交点A2坐标,根据正方形对角线性质表示出B2的坐标,代入对应的解析式即可求出对应的b2的值,写出D2的坐标,代入y2的解析式中可求得a2的值,写出抛物线C2的解析式;再利用相同的方法求抛物线C3的解析式;
(3)①根据图形变换后二次项系数不变得出an=a1=1,由B1坐标(1,1)、B2坐标(3,3)、B3坐标(7,7)得Bn坐标(2n﹣1,2n﹣1),则bn=2(2n﹣1)=2n+1﹣2(n≥1),写出抛物线n解析式.
②先求抛物线C2018和抛物线C2019的交点为(0,0),在交点的两侧观察图形得出y2018与y2019的函数值的大小.
(1)y1=0时,a1x(x﹣b1)=0,
x1=0,x2=b1,
∴A1(b1,0),
由正方形OB1A1D1得:OA1=B1D1=b1,
∴B1(![]() ,
,![]() ),D1(
),D1(![]() ,
,![]() ),
),
∵B1在抛物线c上,则![]() =(
=(![]() )2,
)2,
b1(b1﹣2)=0,
b1=0(不符合题意),b1=2,
∴D1(1,﹣1),
把D1(1,﹣1)代入y1=a1x(x﹣b1)中得:﹣1=﹣a1,
∴a1=1,
故答案为:1,2;
(2)y2=0时,a2x(x﹣b2)=0,
x1=0,x2=b2,
∴A2(b2
由正方形OB2A2D2得:OA2=B2D2=b2,
∴B2(![]() ,
,![]() ),
),
∵B2在抛物线c1上,则![]() =(
=(![]() )2﹣2×
)2﹣2×![]() ,
,
b2(b2﹣6)=0,
b2=0(不符合题意),b2=6,
∴D2(3,﹣3),
把D2(3,﹣3)代入C2的解析式:﹣3=3a2(3﹣6),a2=![]() ,
,
∴C2的解析式:y2=![]() x(x﹣6)=
x(x﹣6)=![]() x2﹣2x,
x2﹣2x,
y3=0时,a3x(x﹣b3)=0,
x1=0,x2=b3,
∴A3(b3,0),
由正方形OB3A3D3得:OA3=B3D3=b3,
∴B3(![]() ,
,![]() ),
),
∵B3在抛物线C2上,则![]() =
=![]() (
(![]() )2﹣2×
)2﹣2×![]() ,
,
b3(b3﹣18)=0,
b3=0(不符合题意),b3=18,
∴D3(9,﹣9),
把D3(9,﹣9)代入C3的解析式:﹣9=9a3(9﹣18),a3=![]() ,
,
∴C3的解析式:y3=![]() x(x﹣18)=
x(x﹣18)=![]() x2﹣2x;
x2﹣2x;
(3)①n的解析式:yn=![]() x2﹣2x(n≥1).
x2﹣2x(n≥1).
②由上题可得:
抛物线C2018的解析式为:y2018=![]() x2﹣2x,
x2﹣2x,
抛物线C2019的解析式为:y2019=![]() x2﹣2x,
x2﹣2x,
∴两抛物线的交点为(0,0);
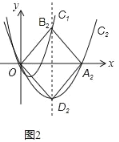
如图4,由图象得:当x≠0时,y2018>y2019.


科目:初中数学 来源: 题型:
【题目】随着襄阳市近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图1所示;种植花卉的利润
成正比例关系,如图1所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
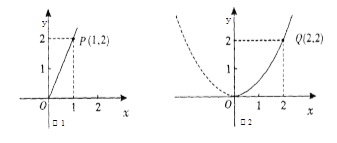
(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以10万元资金投入种植花卉和树木,求他获得的最大利润是多少?
(3)在(2)的条件下,根据对市场需求的调查,这位专业户决定投入种植树木的资金不得高于投入种植花卉的资金,他至少获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有
“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.
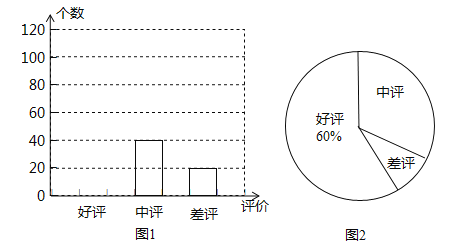
(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
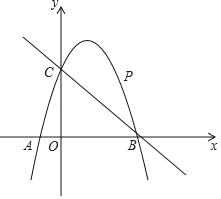
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2
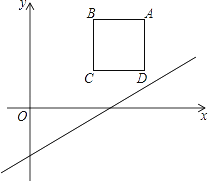
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
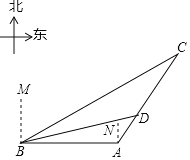
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com