
【题目】阅读:如图1,点P(x,y)在平面直角坐标中,过点P作PA⊥x轴,垂足为A,将点P绕垂足A顺时针旋转角α(0°<α<90°)得到对应点P′,我们称点P到点P′的运动为倾斜α运动.例如:点P(0,2)倾斜30°运动后的对应点为P′(1,![]() ).
).
图形E在平面直角坐标系中,图形E上的所有点都作倾斜α运动后得到图形E′,这样的运动称为图形E的倾斜α运动.
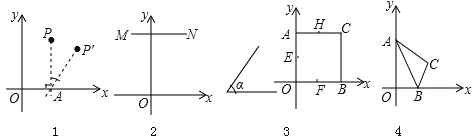
理解
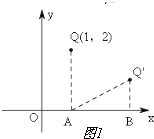
(1)点Q(1,2)倾斜60°运动后的对应点Q′的坐标为 ;
(2)如图2,平行于x轴的线段MN倾斜α运动后得到对应线段M′N′,M′N′与MN平行且相等吗?说明理由.
应用:(1)如图3,正方形AOBC倾斜α运动后,其各边中点E,F,G,H的对应点E′,F′,G′,H′构成的四边形是什么特殊四边形: ;
(2)如图4,已知点A(0,4),B(2,0),C(3,2),将△ABC倾斜α运动后能不能得到Rt△A′B′C′,且∠A′C′B′为直角,其中点A′,B′,C′为点A,B,C的对应点.请求出cosα的值.
【答案】理解(1)(![]() ,1);(2)M′N′与MN平行且相等;应用(1)矩形;(2)
,1);(2)M′N′与MN平行且相等;应用(1)矩形;(2)![]() .
.
【解析】
试题分析:理解:
(1)根据题目中称点P到P′的运动为倾α运动的定义来求Q′的坐标;
(2)根据题目中图形E的倾α运动的定义可以判断M′N′与MN的关系;
应用:
(1)参考理解(2)可得,正方形AOBC旋转后形成菱形,菱形的四边中点组成的四边形是矩形;
(2)先求出A′B′=4=OA′,利用三角函数求得cosα的值.
试题解析:(1)如图1,过点Q作QA⊥x轴,垂足为A,过旋转Q′作x轴的垂线,垂足为B,在Rt△ABQ′中,∠Q′AB=30°,BQ′=1,由勾股定理得AB=![]() ,∴OB=
,∴OB=![]() ,∴Q′的坐标为(
,∴Q′的坐标为(![]() ,1).故答案为:(
,1).故答案为:(![]() ,1);
,1);
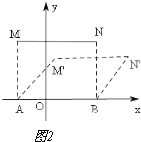
(2)M′N′与MN平行且相等,理由如下:
如图2,分别过点M、N作MA⊥x轴于点A,NB⊥x轴于点B,∴MN∥AB,且MN=AB,由定义可知,M′A∥N′B,M′A=N′B,∴四边M′ABN′是平行四边形,∴M′N′∥AB,M′N′=AB,∴M′N′与MN平行且相等.
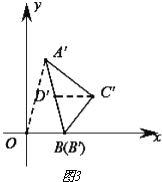
应用:(1)由理解(2)可得,正方形AOBC旋转后形成菱形,菱形的四边中点组成的四边形是矩形.
故答案为:矩形;
(2)能,cosα=![]() .如图3,设AB的中点为D,∴D点坐标为(1,2),∴CD∥x轴,且CD=2,∵D点对应点D′是A′B′中点,C′D′=2,∴C′D′=
.如图3,设AB的中点为D,∴D点坐标为(1,2),∴CD∥x轴,且CD=2,∵D点对应点D′是A′B′中点,C′D′=2,∴C′D′=![]() A′B′,∴A′B′=4=OA′,∵∠α=
A′B′,∴A′B′=4=OA′,∵∠α=![]() ∠OA′B′,∴cosα=
∠OA′B′,∴cosα=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题.
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
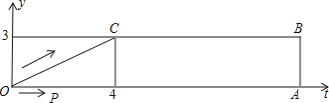
【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对乒乓球、羽毛球、排球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能从中选择一项),随机选取了若干名学生进行抽样调查,并将调查结果绘制成了不完整的统计图.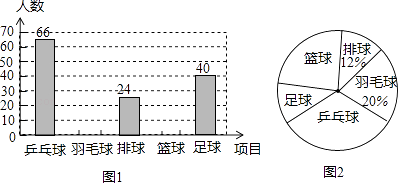
(1)参加调查的学生一共有名,图2中乒乓球所在扇形的圆心角为°;
(2)在图1中补全条形统计图(标上相应数据);
(3)若该校共有2000名同学,请根据抽样调查数据估计该校同学中喜欢足球运动的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com