
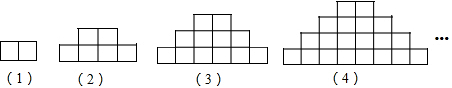
分析 (1)运用倒序求和法计算即可;
(2)根据题意可从第一个同学开始,如果要每两名同学都要握手,第一名同学则需要与剩下的59名同学握手即可,依此类推,握手的总次数为59+58+…+2+1,根据(1)的方法计算即可;
(3)观察不难发现,每一个图形中正方形的个数等于图形序号乘以比序号大1的数,根据此规律解答即可
解答 解:(1)设s=1+2+3+4…+99+100 ①
把上式倒序排列得 s=100+99+…+2+1 ②
①与②两边分别相加得:2s=(1+100)+(2+99)+…+(100+1)=(1+100)×100,
所以 s=$\frac{101×100}{2}$=5050.
(2)∵共有60名同学,若每两名同学互相握手一次,
∴第一名同学则需要与剩下的59名同学握手即可,依此类推,握手的总次数为59+58+…+2+1,
∴全班同学共握手$\frac{(59+1)×59}{2}$=1770(次).
(3)第(1)个图有2个相同的小正方形,2=1×2,
第(2)个图有6个相同的小正方形,6=2×3,
第(3)个图有12个相同的小正方形,12=3×4,
…,
按此规律,第(n)个图有n(n+1)个相同的小正方形.
点评 本题主要考查了数字规律和图形规律问题,根据题干提供的数字规律和方法,类比拓展到实际问题和图形问题,抓住问题的本质善于联系是解决此类问题的关键.此类题目对同学们的能力要求较高,在平时的学习中要不断积累.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5m+2m=7m2 | B. | -2m2•m3=2m5 | C. | (-a2b)3=-a6b3 | D. | (b+2a)(2a-b)=b2-4a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
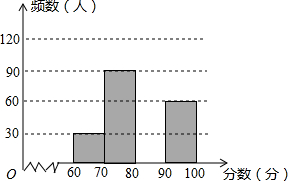 为了解某年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
为了解某年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
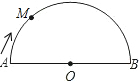 如图,在半圆O上有一动点M,点M从点A出发,沿弧AB、线段BA匀速运动回点A,设OM的长度为y,点M运动的时间为t,则y与t之间的函数图象大致为( )
如图,在半圆O上有一动点M,点M从点A出发,沿弧AB、线段BA匀速运动回点A,设OM的长度为y,点M运动的时间为t,则y与t之间的函数图象大致为( )| A. | 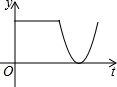 | B. | 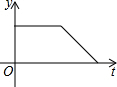 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
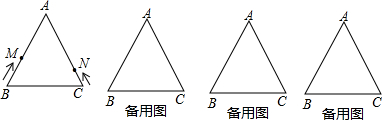
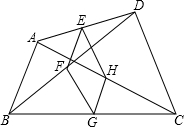 如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?
如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com