
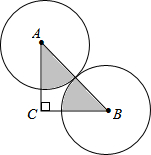
 如图,等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,求图中阴影部分的周长和面积.
如图,等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,求图中阴影部分的周长和面积. 解:∵等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,
解:∵等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,| 90π•52 |
| 360 |
| 25π |
| 4 |
| 2π•5 |
| 4 |
| 5π |
| 2 |
| 5π |
| 2 |
| 25π |
| 4 |


科目:初中数学 来源: 题型:
 某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由.
某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
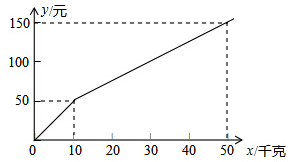 某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示
某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com