
如图1,在菱形ABCD中,∠A=60°.点E,F分别是边AB,AD上的点,且满足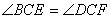 ,连结EF.
,连结EF.
(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证: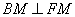 ;
;
(
|

 ,
,
 若
若 点E,F
点E,F 分别是边AB,AD延长线上的点,其它条件不变,结论
分别是边AB,AD延长线上的点,其它条件不变,结论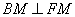 是否仍然成立(不需证明).
是否仍然成立(不需证明). 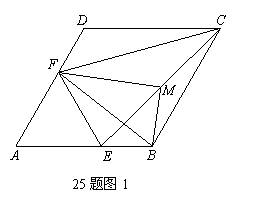
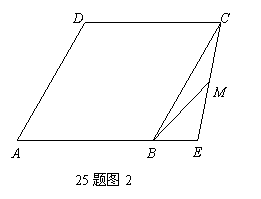
(1)解:∵四边形ABCD是菱形,
∴ AB = AD = BC= DC,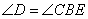 .
.
又∵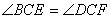 ,
,
∴△CBE≌△CDF.
∴BE=DF.
又∵AB =AD,∴AB-BE =AD-DF,即AE=AF.
又∵∠A=60°,∴△AEF是等边三角形.
∴EF=AF.
∵AF=1,∴EF=1.
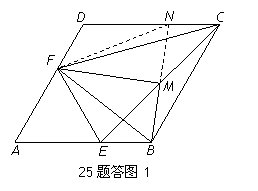
(2)证明:延长BM交DC于点N,连结FN.(如答图)
∵四边形ABCD是菱形,
∴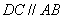 ,
,
∴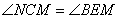 ,
, .
.
∵点M是CE的中点,
∴CM=EM.
∴△CMN≌△EMB.
∴NM=MB,CN=BE.
又∵AB = DC.∴DC-CN=AB-BE, 即DN=AE.
∵ 是等边三角形,∴
是等边三角形,∴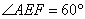 ,EF=AE.
,EF=AE.
 ∴
∴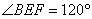 ,EF=DN.
,EF=DN.
∵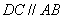 ,∴
,∴ .
.
又∵∠A=60°,∴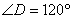 ,
,
∴ .
.
又∵DN=EF,BE=DF.
∴△FDN≌△BEF.
∴FN=FB,
又∵NM=MB,∴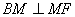 .
.
(3)结论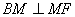 仍然成立
仍然成立


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
某汽车专卖店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知a,b,c为△ABC的三边长,则关于x的一元二次方程4x2+4(a+b)x+c2=0的根的情况( )
A. 有两个不相等的实数根 B. 没有实数根
C. 有两个相等的实数根 D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com