
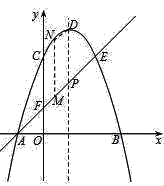
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,顶点为D,过点A的直线与抛物线交于点E,与y轴交于点F,且点B的坐标为(3,0),点E的坐标为(2,3).
(1)求抛物线的解析式;
(2)若点G为抛物线对称轴上的一个动点,H为x轴上一点,当以点C、G、H、F四点所围成的四边形的周长最小时,求出这个最小值及点G、H的坐标;
(3)设直线AE与抛物线对称轴的交点为P,M为直线AE上的任意一点,过点M作MN∥PD交抛物线于点N,以P、D、M、N为顶点的四边形能否为平行四边形?若能,请求点M的坐标;若不能,请说明理由.
【答案】(1)抛物线的解析式为:y=﹣x2+2x+3;(2)G(1,1),H(![]() ,0),四边形CFHG的周长最小值2+2
,0),四边形CFHG的周长最小值2+2![]() ;(3)M的坐标为:M(0,1)或(
;(3)M的坐标为:M(0,1)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据抛物线上的两点列方程组求抛物线y=﹣x2+bx+c中的系数b和c,(2)根据题目的提示可以画出简图,然后表示出以点C、G、H、F四点所围成的四边形的周长,在根据表示出的线段就可以求出最短的周长,对应的点G、H的坐标也可得出;(3)根据题意可以分两种情况讨论,点N在点M的上方或者下方,然后设出点M,根据题目给出的条件是否能将P、D、M、N为顶点的四边形组成平行四边形,可以根据平行四边形对边相等来入手.
(1)∵y=﹣x2+bx+c经过(3,0)和(2,3),
∴![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3,
∴y=﹣(x﹣1)2+4,
∴对称轴为x=1.
当y=0时,﹣x2+2x+3=0,
∴x1=﹣1,x2=3,
∴A(﹣1,0).
当x=0时,y=3,
∴C(0,3)
∴CE=2.OC=3
如图,在y轴的负半轴上取一点I,使得点F点I关于x轴对称,在x轴上取点H,连接HF、HI、HG、GC、GE、则HF=HI.
∵抛物线的对称轴为x=1,
∴点C点E关于对称轴x=1对称,
∴CG=EG.
设直线AE的解析式为y=kx+b,由题意,得
![]() ,
,
解得:![]() ,
,
∴直线AE的解析式为y=x+1.
当x=0时,y=1,
∴F(0,1),
∴OF=1,CF=2.
∵点F与点I关于x轴对称,
∴I(0,﹣1),
∴OI=1,CI=4.
在Rt△CIE中,由勾股定理,得
EI=![]() =2
=2![]() .
.
∵要使四边形CFHG的周长最小,而CF是定值,
∴只要使CG+GH+HF最小即可.
∵CG+GH+HF=EG+GH+HI,
∴只有当EI为一条直线时,EG+GH+HI最小.
设EI的解析式为y=k1x+b1,由题意,得
![]() ,
,
解得:![]() ,
,
∴直线EI的解析式为:y=2x﹣1,
∵当x=1时,y=1,
∴G(1,1).
∵当y=0时,x![]() ,
,
∴H(![]() ,0),
,0),
∴四边形CFHG的周长最小值=CF+CG+GH=CF+EI=2+2![]() ;
;
(3)∵y=﹣x2+2x+3,
∴y=﹣(x﹣1)2+4,
∴D(1,4)
∴直线AE的解析式为y=x+1.
∴x=1时,y=2,
∴P(1,2),
∴PD=2.
∵四边形DPMN是平行四边形,
∴PD=MN=2.
∵点M在AE上,设M(x,x+1),
①当点M在线段AE上时,点N点M的上方,则N(x,x+3),
∵N点在抛物线上,
∴x+3=﹣x2+2x+3,
解得:x=0或x=1(舍去)
∴M(0,1).
②当点M在线段AE或EA的延长线上时,点N在M的下方,则N(x,x﹣1).
∵N点在抛物线上,
∴x﹣1=﹣x2+2x+3,
解得:x=![]() 或x=
或x=![]() ,
,
∴M(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
∴M的坐标为:M(0,1)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 二次函数![]() 的图象是开口向上的抛物线
的图象是开口向上的抛物线
B. 二次函数![]() 的图象必在
的图象必在![]() 轴上方
轴上方
C. 二次函数图象的对称轴是![]() 轴或与
轴或与![]() 轴平行的直线
轴平行的直线
D. 二次函数图象的顶点必在图象的对称轴上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,边长为a、b的矩形,它的周长为14,面积为10,求a2b+3a3b3+ab2的值;

(2)已知a+b=8,ab=16+c2,求(a﹣b+c)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在北部湾经济区农业示范基地采购A,B两种农产品,已知A种农产品每千克的进价比B种多2元,且用24000元购买A种农产品的数量(按重量计)与用18000元购买B种农产品的数量(按重量计)相同.
(1)求A,B两种农产品每千克的进价分别是多少元?
(2)该公司计划购进A,B两种农产品共40吨,并运往异地销售,运费为500元/吨,已知A种农产品售价为15元/kg,B种农产品售价为12元/kg,其中A种农产品至少购进15吨且不超过B种农产品的数量,问该公司应如何采购才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
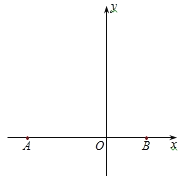
【题目】如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
(1)用尺规作图作出点C,并求出点C的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com