
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,则△A1C1C2 , △A2C2C3 , △A3C3C4 , …,△AnCnCn+1的周长和为 . (n≥2,且n为整数)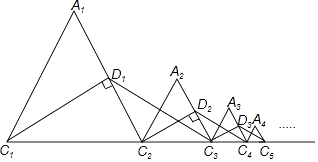
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系.观察图象,你能得到关于这种蔬菜销售情况的哪些信息?答题要求:(1)请提供四条信息;(2)不必求函数的解析式.(注:此题答案不唯一,以上答案仅供参考.若有其它答案,只要是根据图象得出的信息,并且叙述正确都可以)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是必然事件的是( )
A.任意画一个正五边形,它是中心对称图形
B.实数x使式子 ![]() 有意义,则实数x>3
有意义,则实数x>3
C.a,b均为实数,若a= ![]() ,b=
,b= ![]() ,则a>b
,则a>b
D.5个数据分别是:6,6,3,2,1,则这组数据的中位数是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一个等腰梯形的花坛,花坛上底120米,下底180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.
(1)用含x的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2,则四边形PFCG的面积为_______cm2.
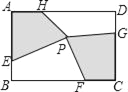
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点坐标分别为A(﹣6,3),B(﹣4,1),C(﹣1,1).
(1)如图1,顺次连接AB,BC,CA,得△ABC.
①点A关于x轴的对称点A1的坐标是 , 点B关于y轴的对称点B1的坐标是;
②画出△ABC关于原点对称的△A2B2C2;
③tan∠A2C2B2=;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为60°,原来的格点A,B,C分别对应新网格中的格点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,得△A′B′C′,则tan∠A′C′B′= . 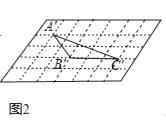
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产上第世博会吉祥物:“海宝”纪念章10万个,质检部门为检测这批纪念章质量的合格情况,从中随机抽查500个,合格499个![]() 下列说法正确的是
下列说法正确的是![]()
![]()
A. 总体是10万个纪念章的合格情况,样本是500个纪念章的合格情况
B. 总体是10万个纪念章的合格情况,样本是499个纪念章的合格情况
C. 总体是500个纪念章的合格情况,样本是500个纪念章的合格情况
D. 总体是10万个纪念章的合格情况,样本是1个纪念章的合格情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
已知:如图,直线BC、AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∠4=∠______(______)
又∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE(等式的性质)
即∴∠3=∠______(等量代换)
∴AD∥BE(______).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com