
【题目】完成下面推理过程:
已知:如图,直线BC、AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∠4=∠______(______)
又∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE(等式的性质)
即∴∠3=∠______(等量代换)
∴AD∥BE(______).

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,则△A1C1C2 , △A2C2C3 , △A3C3C4 , …,△AnCnCn+1的周长和为 . (n≥2,且n为整数)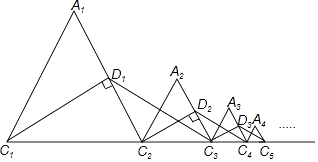
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
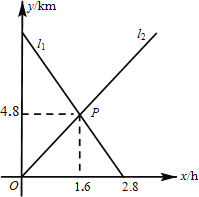
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
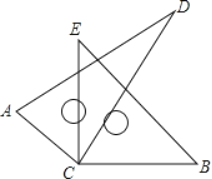
【题目】如图,将两块直角三角板的直角顶点C叠放在一起.
(1)若∠DCE=28°10',求∠ACB的度数;
(2)若∠ACB=148°21',求∠DCE的度数;
(3)直接写出∠ACB与∠DCE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A,B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com