
【题目】在![]() 中,
中,![]() 为直径,CD与
为直径,CD与![]() 相较于点H,弧AC=弧AD
相较于点H,弧AC=弧AD
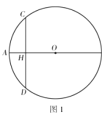
(1)如图1,求证:![]() ;
;
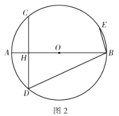
(2)如图2,弧BC上有一点E,若弧CD=弧CE,求证:![]() ;
;
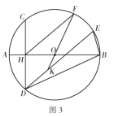
(3)如图3,在(2)的条件下,点F在上,连接![]() ,延长FO交
,延长FO交![]() 于点K,若
于点K,若![]() ,求
,求![]() .
.
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O的两条弦![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() .
.
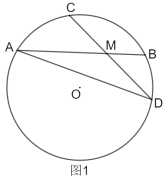
(1)如图1,连接![]() ,求证:
,求证:![]() .
.
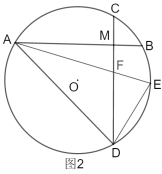
(2)如图2,在![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 是否相等,并说明理由.
是否相等,并说明理由.
②若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应对全球新冠肺炎,满足抗疫物资的需求,某电机公司转型生产![]() 呼吸机和
呼吸机和![]() 呼吸机,每台
呼吸机,每台![]() 呼吸机比每台
呼吸机比每台![]() 呼吸机的生产成本多200元,用5万元生产
呼吸机的生产成本多200元,用5万元生产![]() 呼吸机与用4.5万元生产
呼吸机与用4.5万元生产![]() 呼吸机的数量相等
呼吸机的数量相等
(1)求每台![]() 呼吸机、
呼吸机、![]() 呼吸机的生产成本各是多少元?
呼吸机的生产成本各是多少元?
(2)该公司计划生产这两种呼吸机共50台进行试销,其中![]() 呼吸机为
呼吸机为![]() 台,生产总费用不超过9.8万元,试销时
台,生产总费用不超过9.8万元,试销时![]() 呼吸机每台售价2500元,
呼吸机每台售价2500元,![]() 呼吸机每台售价2180元,公司决定从销售
呼吸机每台售价2180元,公司决定从销售![]() 呼吸机的利润中按每台捐献
呼吸机的利润中按每台捐献![]() 元作为公司捐献国家抗疫的资金,若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元,求
元作为公司捐献国家抗疫的资金,若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 中点为
中点为![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 边上的高
边上的高![]() ,易证
,易证![]() ,从而得到
,从而得到![]() 的面积为
的面积为![]() .
.
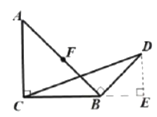
初步探究:如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() 中点为
中点为![]() .将线段
.将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() .用含
.用含![]() 的代数式表示
的代数式表示![]() 的面积,并说明理由.
的面积,并说明理由.
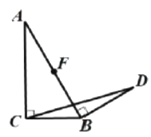
简单应用:如图③,在等腰三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 中点为
中点为![]() .将线段
.将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,直接写出
,直接写出![]() 的面积.(用含
的面积.(用含![]() 的代数式表示)
的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE;
(2)若∠BAC=30°,AB=12,求阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com