
如图,已知直线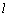 与
与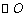 相离,
相离, 于点
于点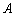 ,交
,交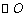 于点
于点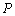 ,点
,点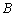 是
是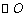 上一点
上一点 ,连接
,连接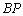 并延长,交直线
并延长,交直线 于点
于点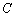 ,使得
,使得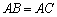 .
.
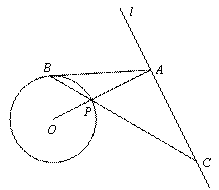
(1)求证: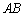 是
是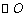 的切线;
的切线;
(2)若 ,
,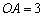 ,求
,求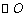 的半径和线段
的半径和线段 的长.
的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连结BE交AC于F,连结FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD②△FED与△DEB③△CFD与△ABG④△ADF与△CFB中相似的为( )

A.①④ B.①② C.②③④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(元)
之间的关系,则下列结论中正确的有( )
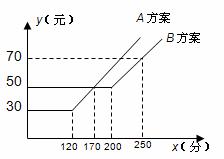
(1)若通话时间少于120分,则A方案比B方案便宜20元
(2)若通话时间超过200分,则B方案比A方案便宜12元
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.
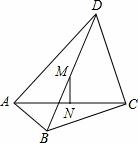
(1)求证:MN⊥AC.
(2)求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为 ( )

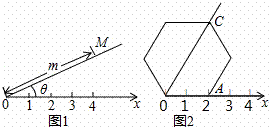
A.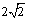 B.
B.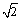 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
(1)观察图形,写出图中与BE相等的线段.
(2)选择图中与BE相等的任意一条线段,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
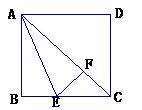
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
A.(60°,4) B.(45°,4) C.(60°,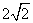 ) D.(50°,
) D.(50°,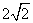 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com