
【题目】如图,正方形![]() 中,
中, ![]() ,点
,点![]() 在边
在边![]() 上,且,
上,且,![]() 将
将![]() 沿
沿![]() 翻折至
翻折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]()
(2)求证:![]() ;
;
(3)求![]() 的面积.
的面积.
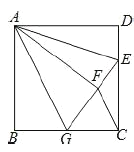
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)由轴对称可以得出AF=AD,∠D=∠AFE=90°,得出∠AFG=90°,根据正方形的性质可以得出AF=AB,根据HL就可以判断△ABG≌△AFG.
(2)由条件可以求出ED的值,设FG=x,则BG=FG=x,CG=6-x,EG=x+2,由勾股定理可以求出x的值,从而可以求出BG和CG的值,得出结论.
(3)过点F作FN⊥CG于点N,可以得出∠FNG=∠DCG=90°,通过证明△GFN∽△GEC,得出![]() ,可以求出FN的值,最后利用三角形的面积公式可以求出其面积.
,可以求出FN的值,最后利用三角形的面积公式可以求出其面积.
(1)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵将![]() 对折得到
对折得到![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
(2)证明: ∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
, ![]() ,
,![]() ,
,
在直角三角形![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,
,
解得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
(3)过点![]() 作
作![]() 于点
于点![]() ,
,
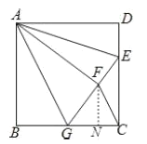
则![]() ,
,
又∵∠FGN=∠EGC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴FN=![]() ,
,
∴S△CGF=![]() CGFN=
CGFN=![]() ×
×![]() ×3=
×3=![]() .
.


科目:初中数学 来源: 题型:
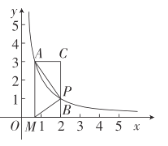
【题目】如图,在平面直角坐标系中,点A(![]() ,3)在反比例函数C:y=
,3)在反比例函数C:y=![]() (x>0)上,点P是反比例函数C:y=
(x>0)上,点P是反比例函数C:y=![]() (x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.
(x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.
(1)求反比例函数的解析式;
(2)若点P(2,n),求PM所在直线的解析式;
(3)PB⊥x轴,B为垂足,CA⊥y轴,BP的延长线交AC于点C,当△AMP与△APC相似时,请写出∠AMP与∠BMP的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
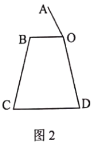
【题目】电水壶采用的是蒸汽智能感应控温原理,具有沸腾后自动断电、防干烧断电的功能.如图1,是一电水壶的实物图.当壶盖打开时,壶盖与闭合时盖面之间的夹角可以抽象为![]() (如图2),壶身侧面与底座(壶盖及底座厚度护理不计)之间的夹角可以抽象为
(如图2),壶身侧面与底座(壶盖及底座厚度护理不计)之间的夹角可以抽象为![]() (如图2)若壶嘴及手柄部分不考虑,量得壶盖和底座的直径分别为
(如图2)若壶嘴及手柄部分不考虑,量得壶盖和底座的直径分别为![]() ,
,![]() ,
,![]() .
.
(1)求底座周长比壶盖周长长多少?(结果保留![]() )
)
(2)若量得![]() ,求壶盖最高点到底座所在平面的距离.
,求壶盖最高点到底座所在平面的距离.
(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .)
.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在期中考试过后,决定给同学们发放奖品.他到对面![]() 文具店看了一下,准备买一些钢笔和笔记本,再给班级购买一个中考倒计时电子显示屏,经预算总共需要1501元,其中电子显示屏的价格为41元.当他付款时才发现他把钢笔和笔记本的单价弄反了,由于王老师购物金额超过1000元,文具店免费赠送了一个电子显示屏.这样实际付款后预算资金还剩余100多元(剩余资金为整数),正好能再购买1支钢笔和1个笔记本,王老师计划购买__________件奖品.
文具店看了一下,准备买一些钢笔和笔记本,再给班级购买一个中考倒计时电子显示屏,经预算总共需要1501元,其中电子显示屏的价格为41元.当他付款时才发现他把钢笔和笔记本的单价弄反了,由于王老师购物金额超过1000元,文具店免费赠送了一个电子显示屏.这样实际付款后预算资金还剩余100多元(剩余资金为整数),正好能再购买1支钢笔和1个笔记本,王老师计划购买__________件奖品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC﹣CD﹣DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图2所示,则y的最大值是( )
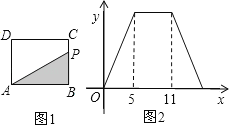
A.55B.30C.16D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30![]() .小东骑自行车以300
.小东骑自行车以300![]() 的速度直接回家,两人距家的路程
的速度直接回家,两人距家的路程![]() 与各自离开出发地的时间
与各自离开出发地的时间![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)家与图书馆之间的路程为__________![]() ,小玲步行的速度为__________
,小玲步行的速度为__________![]() ;
;
(2)求小东距家的路程![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(3)求两人出发后多长时间相遇.
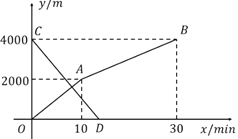
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量底面为圆形的古塔的高度,小红和小明应用不同方法对其展开了研究,以下是他们各自的研究方法和研究数据:
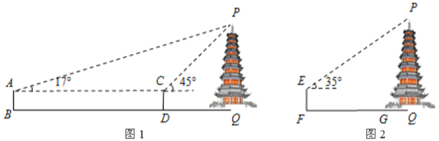
小红:如图1,测角仪![]() ,
,![]() 的高度均为
的高度均为![]() ,分别测得古塔顶端的仰角为
,分别测得古塔顶端的仰角为![]() ,
,![]() ,测角仪底端的距离
,测角仪底端的距离![]() 为
为![]() .
.
小明:如图2,测角仪![]() 的高度为
的高度为![]() ,测得古塔顶端的仰角为
,测得古塔顶端的仰角为![]() ,测角仪所在位置与古塔底部边缘的最短距离
,测角仪所在位置与古塔底部边缘的最短距离![]() 为
为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )小明利用测得的数据计算古塔高度
)小明利用测得的数据计算古塔高度![]() .
.
问题1:指出小明计算过程中的错误之处;
问题2:利用两人的测量数据,求出古塔底面圆的半径![]() (结果精确到
(结果精确到![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com