
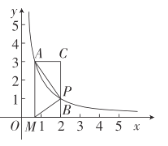
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(![]() ��3)�ڷ���������C��y=
��3)�ڷ���������C��y=![]() (x>0)�ϣ���P�Ƿ���������C��y=
(x>0)�ϣ���P�Ƿ���������C��y=![]() (x>0)��-���㣬����AP����M��x���ϣ�������MP��AP������ΪP��
(x>0)��-���㣬����AP����M��x���ϣ�������MP��AP������ΪP��
(1)���������Ľ���ʽ��
(2)����P(2��n)����PM����ֱ�ߵĽ���ʽ��
(3)PB��x�ᣬBΪ���㣬CA��y�ᣬBP���ӳ��߽�AC�ڵ�C������AMP����APC����ʱ����д����AMP���BMP��������ϵ����˵�����ɣ�
���𰸡���1��y=![]() ����2��y=
����2��y=![]() x��
x��![]() ����3����AMP=��BMP���AMP+��BMP=90�������ɼ�������
����3����AMP=��BMP���AMP+��BMP=90�������ɼ�������
��������
��1��k=![]() ��3=2���ʷ����������Ľ���ʽΪ��y=
��3=2���ʷ����������Ľ���ʽΪ��y=![]() ��
��
��2���������P�����꣬Ȼ��õ���C�����꣬��֤����APC����PMB���õ���M�����꣬���ݴ���ϵ�������������ֱ�ߵĽ���ʽ.
��3���������������ε����ʣ��ֳ���������������ۣ����ɵõ���.
�⣺��1����k=![]() ��3=2��
��3=2��
�෴���������Ľ���ʽΪ��y=![]() ��
��
(2)��P��2��n���ڷ���������C��y=![]() (x>0)��ͼ���ϣ�
(x>0)��ͼ���ϣ�
��n=1��
��P(2��1)��
��PB��x�ᣬMP��AP��CA��y�ᣬ
��C(2��3)����C=��APM=��MBP=90����
���APC����MPB=90������PMB����MPB=90��
���APC=��PMB��
����APC����PMB
��![]() =
=![]() ��
��
��MB=![]() ��M(
��M(![]() ��0)
��0)
��PM����ֱ�ߵĽ���ʽΪ��y=kxʮb��
��P(2��1)��M(![]() ��0)����ã�
��0)����ã�
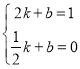 ��
��
��ã�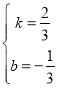 ��
��
��y=![]() x��
x��![]() ��
��
(3)����AMP����APC����ʱ���֡���APC����PMB��
��������������PMB���ƣ�
���AMP=��BMP���AMP=��PBM��
���AMP=��BMP���AMP+��BMP=90����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ������B��3��0����C��0��-2����ֱ��L��
������B��3��0����C��0��-2����ֱ��L��![]() ��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A�غϣ���
��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A�غϣ���
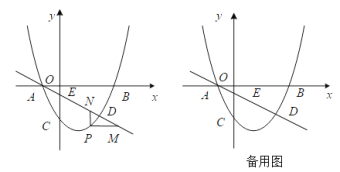
��1���������ߵĽ���ʽ��
��2������P��ֱ��L�·�ʱ������P��PM��x�ύL�ڵ�M��PN��y�ύL�ڵ�N����PM+PN�����ֵ��
��3����FΪֱ��L�ϵĵ㣬��E��C��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() ����
����![]() ���ӳ�����ȡһ��
���ӳ�����ȡһ��![]() ��ʹ
��ʹ![]() ��
��![]() ���ӳ��߽�
���ӳ��߽�![]() ���ӳ�����
���ӳ�����![]() ��
��
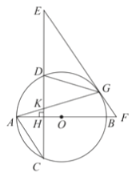
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2������![]() ����
����![]() ʱ��
ʱ��
����֤��![]() ��
��
����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
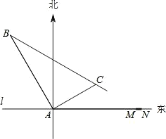
����Ŀ����ij�ɻ�����������ĵ��� l ����һ��Ϊ 1km �ķɻ��ܵ� MN����ͼ�������ܵ� MN�������� 14.5 ǧ�״���һ�۲�վ A��ijʱ�̲��һ������ֱ�߽���ķɻ�λ�ڵ� A �ı�ƫ��30��������� A ��� 15 ǧ�� B �������� 1 ���ӣ��ֲ�ø÷ɻ�λ�ڵ� A �ı�ƫ�� 60��������� A ��� 5![]() ǧ�� C ����
ǧ�� C ����
��1���÷ɻ����е��ٶ��Ƕ���ǧ��/Сʱ��������������ţ�
��2������÷ɻ����ı亽��������У���ô�ɻ��ܷ������ܵ� MN ֮�䣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ա���ͬѧ��ҵ����Ȥ���ý�����һ�ε��飬�����ݲɼ��������ݣ������������ͼ1��ͼ2��
�������ͼ���ṩ����Ϣ������������⣺
��1����ͼ1�У������黭�����ֵ�ͼ�β���������
��2����ͼ2�У��������������������Ӧ��Բ�ĽǵĶ��������ֱ�д�������������������黭������������������ռ����ѧ�����İٷ�����
��3���۲�ͼ1��ͼ2�����ܵó���Щ���ۣ�ֻҪд��һ�����ۣ���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������300ǧ�ף�һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵ���ͼ����ͼ���߶�OA��ʾ������ؾ���y��ǧ�ף���ʱ��x��Сʱ��֮��ĺ���ͼ������BCD��ʾ�γ���ؾ���y��ǧ�ף���ʱ��x��Сʱ��֮��ĺ���ͼ�������ͼ�����µ����⣺
��1��������ؾ���y�����ף���ʱ��x��Сʱ��֮��ĺ���ʽΪ�� ����
��2�����γ����������ʱ�����ʱx��ֵ��
��3����������ʻ�����У����γ���������20ǧ��ʱ����x��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ڣ���������ͬһ��ֱ���ϵĵ�![]() ����ͼ��ʾ������
����ͼ��ʾ������![]() ����
����![]() �ľ��������
�ľ��������![]() (
(![]() ����)������
Ϊ����)������![]() �ľ������
�ľ������![]() �����е����ͼ��
�����е����ͼ��![]() ��
��![]() ��ƽ���߽�ͼ��
��ƽ���߽�ͼ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
��1����֤��![]() ��
��
��2������![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ӳ�
���ӳ�![]() ��ͼ��
��ͼ��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() ����ֱ��
����ֱ��![]() ��ͼ��
��ͼ��![]() �Ĺ����������
�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCO�У�A��1��2����B��5��2������ABCO��O����ʱ�뷽����ת90����A��B��C��O��λ�ã����B���������ǣ�������

A.����2��4��B.����2��5��C.����1��5��D.����1��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
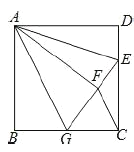
����Ŀ����ͼ��������![]() �У�
�� ![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ��ң�
�ϣ��ң�![]() ��
��![]() ��
��![]() ������
������![]() ���ӳ�
���ӳ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��
��1����֤��![]()
��2����֤��![]() ��
��
��3����![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com