
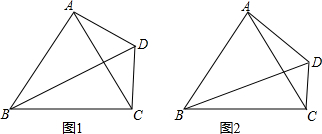
分析 (1)先根据∠BDC=∠BAC=60°得出A、B、C、D四点共圆,进而得出△ABD为含30°角的直角三角形,即可得出结论;
(2)由A、B、C、D四点共圆,得出△BCD∽△BOC,再根据相似的性质可得结论.
解答 证明:(1)∵∠BDC=∠BAC=60°,
∴A、B、C、D四点共圆,
又∵AD=CD
∴∠ABD=∠CBD=∠CAD=30°,
∴△ABD为含30°角的直角三角形,
∴BD=2AD=2CD,
(2)设AC,BD交于O,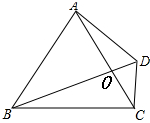
∵A、B、C、D四点共圆,
∴∠ADB=∠BDC=∠BAC=60°
∴BD为∠ADC的角平分线,
即$\frac{AD}{CD}=\frac{AO}{CO}=m$
设CO=1,则AO=m,BC=AC=1+m
∵∠ACB=∠BDC=60°,∠DBC=∠CBO,
∴△BCD∽△BOC,
∴$\frac{BD}{CD}=\frac{BC}{CO}=1+m$.
点评 本题主要考查的是四点共圆的性质与判定,以及相似三角形性质与判定,根据条件得出A、B、C、D四点共圆和△BCD∽△BOC是解决本题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
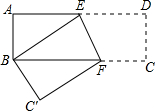 将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
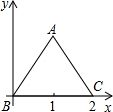 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
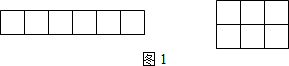
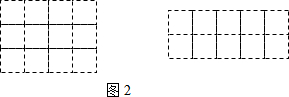
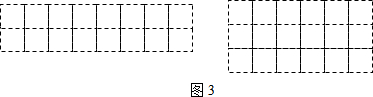
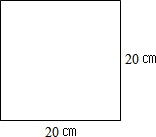
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是半圆的直径,点O为圆心,点P沿OA→$\widehat{AB}$→BO匀速运动一周,设OP的长为s,运动时间为t,则s与t的函数关系图象大致是( )
如图,AB是半圆的直径,点O为圆心,点P沿OA→$\widehat{AB}$→BO匀速运动一周,设OP的长为s,运动时间为t,则s与t的函数关系图象大致是( )| A. | 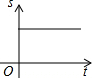 | B. | 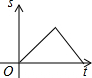 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com