
【题目】已知,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]()
![]() 两点,顶点为
两点,顶点为![]() .
.
(1)当![]() ,
,![]() 时,求线段
时,求线段![]() 的长度;
的长度;
(2)当![]() ,若点
,若点![]() 到
到![]() 轴的距离与点
轴的距离与点![]() 到
到![]() 轴的距离相等,求该抛物线的解析式;
轴的距离相等,求该抛物线的解析式;
(3)若![]() ,当
,当![]() 时,
时,![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
【答案】(1)2;(2)![]() (P在第一象限),
(P在第一象限),![]() (P在第四象限);(3)m的值为
(P在第四象限);(3)m的值为![]() 或10+2
或10+2![]()
【解析】
(1)把a=1,m=2代入函数解析式,得到y=x2﹣4x+3,求出A、B两点坐标,问题得解;
(2)把![]() 代入函数解析式,得到y=2x2﹣4mx+2m2+2m﹣5=
代入函数解析式,得到y=2x2﹣4mx+2m2+2m﹣5=![]() ,确定点P的坐标(m,2m-5),即点P在直线 y=2x-5上,根据点P到x轴的距离与点P到y轴的距离相等,分点P在第一象限和第四象限讨论即可;
,确定点P的坐标(m,2m-5),即点P在直线 y=2x-5上,根据点P到x轴的距离与点P到y轴的距离相等,分点P在第一象限和第四象限讨论即可;
(3)当a=![]() ,抛物线的解析式为y=
,抛物线的解析式为y=![]() (x﹣m)2+2m﹣5.分三类讨论①当m>2m﹣2,即m<2时,
(x﹣m)2+2m﹣5.分三类讨论①当m>2m﹣2,即m<2时,![]() (2m﹣2﹣m)2+2m﹣5=2;②当2m﹣5≤m≤2m﹣2,即2≤m≤5时,2m﹣5=2;③当m<2m﹣5,即m>5时,
(2m﹣2﹣m)2+2m﹣5=2;②当2m﹣5≤m≤2m﹣2,即2≤m≤5时,2m﹣5=2;③当m<2m﹣5,即m>5时,![]() (2m﹣5﹣m)2+2m﹣5=2,分别解方程,舍去不合题意者,问题得解.
(2m﹣5﹣m)2+2m﹣5=2,分别解方程,舍去不合题意者,问题得解.
解:(1)当a=1,m=2时;y=x2﹣4x+3
当y=0时,x2﹣4x+3=0;![]()
AB=3-1=2
(2)y=2x2﹣4mx+2m2+2m﹣5=![]()
∵顶点为P,∴P(m,2m-5)
∴点P在直线 y=2x-5上
∵点P到x轴的距离与点P到y轴的距离相等
∴当点P在第一象限时,m=2m-5,m=5,该抛物线的解析式为![]()
当点P在第四象限时,m=-(2m-5),m=![]() ,该抛物线的解析式为
,该抛物线的解析式为![]()
(3)a=![]() ,抛物线的解析式为y=
,抛物线的解析式为y=![]() (x﹣m)2+2m﹣5.
(x﹣m)2+2m﹣5.
分三种情况考虑:
①当m>2m﹣2,即m<2时,有![]() (2m﹣2﹣m)2+2m﹣5=2,
(2m﹣2﹣m)2+2m﹣5=2,
整理,得:m2﹣14m+39=0,
解得:m1=7﹣![]() (舍去),m2=7+
(舍去),m2=7+![]() (舍去);
(舍去);
②当2m﹣5≤m≤2m﹣2,即2≤m≤5时,有2m﹣5=2,
解得:m=![]() ;
;
③当m<2m﹣5,即m>5时,有![]() (2m﹣5﹣m)2+2m﹣5=2,
(2m﹣5﹣m)2+2m﹣5=2,
整理,得:m2﹣20m+60=0,
解得:m3=10﹣2![]() (舍去),m4=10+2
(舍去),m4=10+2![]() .
.
综上所述:m的值为![]() 或10+2
或10+2![]() .
.


科目:初中数学 来源: 题型:
【题目】2020年春节前夕,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩等防护用品成了年货,供应紧张.某药店用2000元购进某品牌的一批口罩后,供不应求,又用5000元购进这种口罩,第二批口罩的数量是第一批的2倍,但进货单价比第一批贵2元.
(1)第一批口罩进货单价多少元?
(2)若两次购进口罩按同一价格销售,两批全部售完后,获利不少于2000元,那么销售单价至少为多少元?
(3)由于党的好政策,爱心工人加班加点地生产,口罩变得不再紧俏,药店第三批进货单价比第一批便宜1元,若按照(2)中销售单价出售,每天可以售出60个,药店为了促销,决定降低一定的价格,每降低一元,每天多售出20个,问单价定为多少时,每天利润最大?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
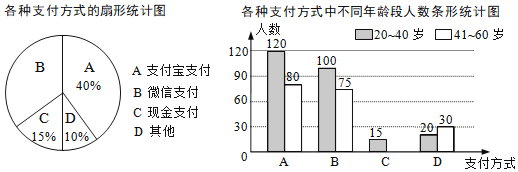
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 的顶点是A(1,3),将OA绕点O逆时针旋转
的顶点是A(1,3),将OA绕点O逆时针旋转![]() 后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.

(1)求抛物线的解析式;
(2)P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与![]() 的边分别交于M,N两点,将
的边分别交于M,N两点,将![]() 以直线MN为对称轴翻折,得到
以直线MN为对称轴翻折,得到![]() .
.
设点P的纵坐标为m.
①当![]() 在
在![]() 内部时,求m的取值范围;
内部时,求m的取值范围;
②是否存在点P,使![]() ,若存在,求出满足m的值;若不存在,请说明理由.
,若存在,求出满足m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
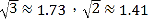
查看答案和解析>>
科目:初中数学 来源: 题型:
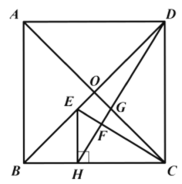
【题目】如图,在边长为1的正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于O.点.H为边
相交于O.点.H为边![]() 上的点,过点H作
上的点,过点H作![]() ,交线段
,交线段![]() 于点E,连接
于点E,连接![]() 交
交![]() 于点F,交
于点F,交![]() 于点G.若
于点G.若![]() ,则
,则![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
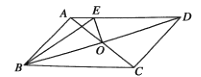
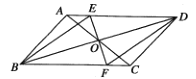
【题目】如图,在平行四边形![]() 中,
中,![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() .
.
(1)如图,求证:![]() 平分
平分![]() ;
;
(2)如图,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,在不添加任何辅助线的条件下,请直接写出面积为
,在不添加任何辅助线的条件下,请直接写出面积为![]() 面积2倍的三角形.
面积2倍的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com