Question

【题目】如图，在中，，，点为的中点，点、分别在、上，且，下列结论：①是等腰直角三角形；②；③；④.其中正确的是( )

A.①②④B.②③④C.①②③D.①②③④

Answer 1

【答案】C

【解析】

根据等腰直角三角形的性质以及斜边上的中线的性质，易证得△CDF≌△ADE，即可判断①②；利用SSS即可证明△BDE△ADF，故可判断③；利用等量代换证得，从而可以判断④.

∵△ABC为等腰直角三角形，且点在D为BC的中点，
∴CD=AD=DB，AD⊥BC，∠DCF=∠B=∠DAE=45°，
∵∠EDF=90，

又∵∠CDF+∠FDA=∠CDA=90，

∠EDA+∠EDA=∠EDF=90，

∴∠CDF=∠EDA，

在△CDF和△ADE中，

，
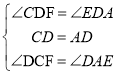∴△CDF≌△ADE，

∴DF=DE，且∠EDF=90，故①是等腰直角三角形，正确；

CF=AE，故②正确；

∵AB=AC，又CF=AE，

∴BE=AB-AE=AC-CF=AF，

在△BDE和△ADF中，

，

∴△BDE△ADF，故③正确；

∵CF=AE，

∴，故④错误；

综上：①②③正确

故选：．