
 如图,已知△ABC为等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
如图,已知△ABC为等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
|


科目:初中数学 来源: 题型:
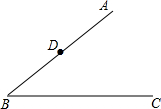 如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:
如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:
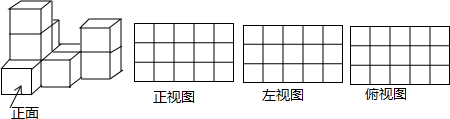
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )A、
| ||
B、
| ||
C、
| ||
| D、300πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2400元 |
| B、2200元 |
| C、2000元 |
| D、1800元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
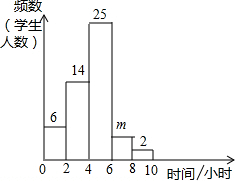 小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了如图所示的频率分布直方图.若从参加课外活动时间在6~10小时的5名学生中随机选取2人,则其中至少有1人课外活动时间在8~10小时的概率为( )
小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了如图所示的频率分布直方图.若从参加课外活动时间在6~10小时的5名学生中随机选取2人,则其中至少有1人课外活动时间在8~10小时的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com