
【题目】(问题实验)如图①,在地面![]() 上有两根等长立柱
上有两根等长立柱![]() ,
,![]() 之间悬挂一根近似成抛物线
之间悬挂一根近似成抛物线![]() 的绳子.
的绳子.
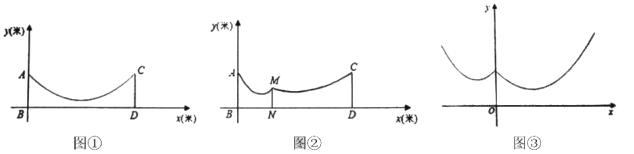
(1)求绳子最低点到地面的距离;
(2)如图②,因实际需要,需用一根立柱![]() 撑起绳子.
撑起绳子.
①若在离![]() 为4米的位置处用立柱
为4米的位置处用立柱![]() 撑起,使立柱左侧的抛物线的最低点距
撑起,使立柱左侧的抛物线的最低点距![]() 为1米,离地面1.8米,求
为1米,离地面1.8米,求![]() 的长;
的长;
②将立柱![]() 来回移动,移动过程中,在一定范围内,总保持立柱
来回移动,移动过程中,在一定范围内,总保持立柱![]() 左侧抛物线的形状不变,其函数表达式为
左侧抛物线的形状不变,其函数表达式为![]() ,当抛物线最低点到地面距离为0.5米时,求
,当抛物线最低点到地面距离为0.5米时,求![]() 的值.
的值.
(问题抽象)如图③,在平面直角坐标系中,函数![]() 的图像记为
的图像记为![]() ,函数
,函数![]() 的图像记为
的图像记为![]() ,其中
,其中![]() 是常数,图像
是常数,图像![]() 、
、![]() 合起来得到的图像记为
合起来得到的图像记为![]() .
.
设![]() 在
在![]() 上的最低点纵坐标为
上的最低点纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
【答案】【问题实验】(1)![]() 米;(2)①
米;(2)①![]() 米;②
米;②![]() ;【问题抽象】
;【问题抽象】![]() 或
或![]() .
.
【解析】
【问题实验】
(1)先把抛物线转化为顶点式,进而可得答案;
(2)①先求出点A坐标,由题意可设![]() ,然后把点A坐标代入即可求出a的值,再求当x=4时对应的y的值即为所求;
,然后把点A坐标代入即可求出a的值,再求当x=4时对应的y的值即为所求;
②根据题意可确定:该抛物线的顶点坐标为![]() ,然后把该点代入抛物线的解析式可得关于m的方程,解方程并结合抛物线对称轴的位置即可求出结果;
,然后把该点代入抛物线的解析式可得关于m的方程,解方程并结合抛物线对称轴的位置即可求出结果;
【问题抽象】
当![]() 时,对
时,对![]() ,确定其对称轴为直线
,确定其对称轴为直线![]() 后,由于
后,由于![]() ,可分
,可分![]() 与
与![]() 两种情况,根据抛物线的性质确定其最小值y0,然后由
两种情况,根据抛物线的性质确定其最小值y0,然后由![]() 即可得到关于m的不等式组,解不等式组即可求出结果;当x<0时,对于
即可得到关于m的不等式组,解不等式组即可求出结果;当x<0时,对于![]() ,确定其对称轴是直线x=m后,仿照上面的思路求解即可.
,确定其对称轴是直线x=m后,仿照上面的思路求解即可.
解:【问题实验】(1)![]() ,
,
∴绳子最低点到地面的距离是![]() 米;
米;
(2)对![]() ,当x=0时,y=3,∴A(0,3),
,当x=0时,y=3,∴A(0,3),
①由题意可知:MN左侧的抛物线的顶点为(3,1.8),于是设抛物线的解析式为![]() ,
,
把![]() 代入,得:
代入,得:![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 米;
米;
②由于![]() 的对称轴是直线x=m,所以该抛物线的顶点坐标为
的对称轴是直线x=m,所以该抛物线的顶点坐标为![]() ,
,
把![]() 代入
代入![]() 中,
中,![]() ,
,
解得:![]() ,
,![]() ,
,
由于抛物线的对称轴在y轴右侧,∴![]() ;
;
【问题抽象】
由题意知:抛物线M1、M2均过定点(0,3),当m≥0时,M1的最低点为(0,3),此时,抛物线M的最低点在M2上.当![]() 时,对M2:
时,对M2:![]() ,其对称轴是直线
,其对称轴是直线![]() .
.
①当![]() ,即
,即![]() 时,
时,
∵当![]() 时,y随x的增大而减小,∴当x=2时,y最小,此时
时,y随x的增大而减小,∴当x=2时,y最小,此时![]() ,
,
∵![]() ,∴
,∴![]() ,解得:
,解得:![]() ;
;
②当![]() ,即
,即![]() 时,
时,
∵x的范围是![]() ,∴当x=2m时y最小,此时
,∴当x=2m时y最小,此时![]() ,
,
∵![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,
∵![]() ,∴此种情况的m的值不存在;
,∴此种情况的m的值不存在;
当m<0时,M2的最低点为(0,3),此时,抛物线M的最低点在M1上,当x<0时,对于M1:![]() ,其对称轴是直线x=m.
,其对称轴是直线x=m.
③当![]() 时,
时,
∵当![]() 时,y随x的增大而增大,∴当x=﹣3时,y最小,此时
时,y随x的增大而增大,∴当x=﹣3时,y最小,此时![]() ,
,
∵![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,
∵![]() ,所以m的范围是
,所以m的范围是![]() ;
;
④当![]() 时,
时,
∵x的范围是![]() ,∴当x=m时,y最小,此时
,∴当x=m时,y最小,此时![]() ,
,
∵![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,
∵![]() ,∴
,∴![]() ;
;
综上所述,m的取值范围是:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场销售一种笔记本,进价为每本10元.试营销阶段发现:当销售单价为12元时,每天可卖出100本,如调整价格,每涨价1元,每天要少卖出10本.设该笔记本的销售单价为![]() 元,每天获得的销售利润为
元,每天获得的销售利润为![]() 元.
元.
(1)当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当![]() 时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
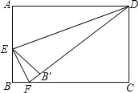
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形![]() 的顶点C与原点O重合,点B落在y轴正半轴上,点A、D落在第一象限内,且D点坐标为
的顶点C与原点O重合,点B落在y轴正半轴上,点A、D落在第一象限内,且D点坐标为![]() .
.
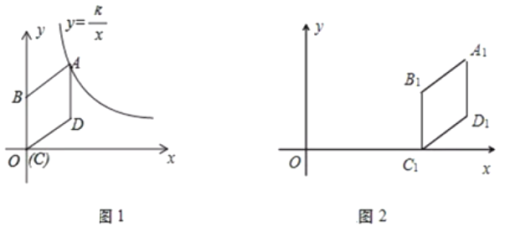
(1)如图1,若反比例函数![]() (
(![]() )的图象经过点A,求k的值;
)的图象经过点A,求k的值;
(2)菱形![]() 向右平移t个单位得到菱形
向右平移t个单位得到菱形![]() ,如图2.
,如图2.
①请直接写出点![]() 、
、![]() 的坐标(用合1的代数式表示):
的坐标(用合1的代数式表示):![]() 、
、![]() ;
;
②是否存在反比例函数![]() (
(![]() ),使得点
),使得点![]() 、
、![]() 同时落在
同时落在![]() (
(![]() )的图象上?若存在,求n的值;若不存在,请说明理由.
)的图象上?若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进![]() 两种商品,已知购进
两种商品,已知购进![]() 种商品5件和
种商品5件和![]() 种商品4件共需300元;若购进
种商品4件共需300元;若购进![]() 种商品6件和
种商品6件和![]() 种商品8件共需440元;
种商品8件共需440元;
(1)求![]() 两种商品每件的进价分别为多少元?
两种商品每件的进价分别为多少元?
(2)若该商店,![]() 种商品每件的售价为48元,
种商品每件的售价为48元,![]() 种商品每件的售价为31元,且商店将购进
种商品每件的售价为31元,且商店将购进![]() 共50件的商品全部售出后,要获得的利润超过348元,求
共50件的商品全部售出后,要获得的利润超过348元,求![]() 种商品至少购进多少件?
种商品至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
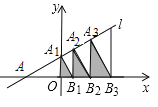
【题目】如图,直线l:y=![]() 分别交x轴、y轴于点A和点A1,过点A1作A1B1⊥l,交x轴于点B1,过点B1作B1A2⊥x轴,交直线l于点A2;过点A2作A2B2⊥l,交x轴于点B2,过点B2作B2A3⊥x轴,交直线l于点A3;依此规律...若图中阴影△A1OB1的面积为S1,阴影△A2B1B2的面积S2,阴影△A3B2B3的面积S3...,则Sn=__________.
分别交x轴、y轴于点A和点A1,过点A1作A1B1⊥l,交x轴于点B1,过点B1作B1A2⊥x轴,交直线l于点A2;过点A2作A2B2⊥l,交x轴于点B2,过点B2作B2A3⊥x轴,交直线l于点A3;依此规律...若图中阴影△A1OB1的面积为S1,阴影△A2B1B2的面积S2,阴影△A3B2B3的面积S3...,则Sn=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com