
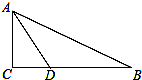
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
(1)动手操作:利用尺规作圆O,使圆O经过点A、D,且圆心O在AB上;并标出圆O与AB的另一个交点E,与AC的另一个交点F(保留作图痕迹,不写作法)
(2)综合应用:在你所作的图中.
①判断直线BC与圆O的位置关系,并说明理由;
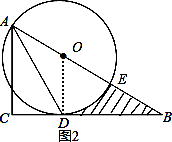
②如果∠BAC=60°,CD=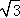 ,求线段BD、BE与劣弧DE所围成的图形面积(结果保留根号和π).
,求线段BD、BE与劣弧DE所围成的图形面积(结果保留根号和π).
【考点】作图—复杂作图;直线与圆的位置关系;扇形面积的计算.
【分析】(1)根据题意得:O点应该是AD垂直平分线与AB的交点;
(2)①由∠BAC的角平分线AD交BC边于D,与圆的性质可证得AC∥OD,又由∠C=90°,则问题得证;
②设⊙O的半径为r.则在Rt△OBD中,利用勾股定理列出关于r的方程,通过解方程即可求得r的值;然后根据扇形面积公式和三角形面积的计算可以求得线段BD、BE与劣弧DE所围成的图形面积为:S△ODB﹣S扇形ODE=2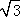 ﹣
﹣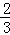 π.
π.
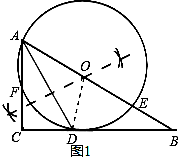
【解答】解:(1)如图1;
(2)①直线BC与⊙O的位置关系为相切.理由如下:
如图1,连接OD,
∵OA=OD,
∴∠OAD=∠ADO,
∵∠BAC的角平分线AD交BC边于D,
∴∠CAD=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
即直线BC是⊙O的切线,
∴直线BC与⊙O的位置关系为相切;
②如图2,
∵∠BAC的角平分线AD交BC于D,∠BAC=60°,∠C=90°,
∴∠CAD=∠DAB=30°,∠B=30°,
∴∠DAB=∠B=30°,
∴BD=AD.
∵在Rt△ADC中,∠C=90°,∠CAD=30°,CD=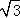 ,
,
∴AD=2CD=2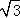 ,AC=
,AC=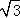 CD=3,
CD=3,
∴BD=2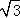 ,AB=2AC=6.
,AB=2AC=6.
设⊙O的半径为r,
在Rt△OBD中,OD2+BD2=OB2,
即r2+(2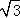 )2=(6﹣r)2,
)2=(6﹣r)2,
解得r=2,OB=6﹣r=4,
∵∠ODB=90°,∠B=30°,
∴∠DOB=60°,
∴S扇形ODE=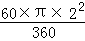 =
=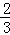 π,
π,
S△ODB= OD•BD=
OD•BD= ×2×2
×2×2 =2
=2 ,
,
∴线段BD、BE与劣弧DE所围成的图形面积为:S△ODB﹣S扇形ODE=2 ﹣
﹣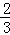 π.
π.
【点评】此题考查了作图﹣复杂作图,切线的判定与性质以及扇形面积与三角形面积的求解方法等知识,注意数形结合思想的应用是解答此题的关键.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
某商场有甲、乙两箱不同价格的糖果,甲糖果为mkg,单价为a元/kg;乙糖果为nkg,单价为b元/kg.商场决定对两种糖果混合出售,混合单价为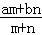 元/kg.(混合单价=
元/kg.(混合单价=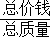 ).
).
(1)若a=30,m=30,b=25,n=20,则混合后的糖果单价为 28 元/kg;
(2)若a=30,商场现在有单价为24元/kg的这种混合糖果100kg,商场想通过增加甲种糖果,把混合后的单价提高15%,问应加入甲种糖果多少千克?
(3)若m=40,n=60,从甲、乙两箱取出相同质量的糖果,将甲箱取出的糖果与乙箱剩余的糖果混合:将乙箱取出的糖果与甲箱剩余的混合,两种混合糖果的混合单价相同,求甲、乙两箱取出多少糖果.
查看答案和解析>>
科目:初中数学 来源: 题型:
小明四等分弧AB,他的作法如下:
(1)连接AB(如图);
(2)作AB的垂直平分线CD交弧AB于点M,交AB于点T;
(3)分别作AT,TB的垂直平分线EF,GH,交弧AB于N,P两点,则N,M,P三点把弧AB四等分.
你认为小明的作法是否正确: ,理由是 .
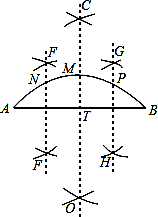
查看答案和解析>>
科目:初中数学 来源: 题型:
.以下列各组线段为边,能组成三角形的是
A.1cm,2cm,3cm B.2cm,3cm,6cm C.8cm,6cm,4cm D.12cm,5cm,6cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com