
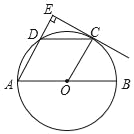
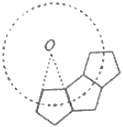
【题目】如图所示,AB是⊙O的直径,点D是弧AC的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)若CE=![]() ,求⊙O的半径长.
,求⊙O的半径长.
【答案】(1)详见解析;(2)2.
【解析】
(1)由点D是弧AC的中点,连接OC,可得圆心角等,再利用已知,∠COB=60°,可得∠AOD和∠COD均为60°,从而△AOD和△COD均为等边三角形,
进一步推出OC∥AE,然后利用已知CE⊥AD,可得∠OCE=90°,从而CE为⊙O的切线.
(2)利用△AOD和△COD均为等边三角形,推出∠ECD等于30°,在直角三角形ECD中,已知CE=![]() ,利用三角函数可以求出CD,从而求得半径.
,利用三角函数可以求出CD,从而求得半径.
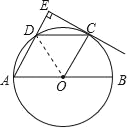
(1)证明:连接OD,如图,
∵点D是弧AC的中点,
∴∠AOD=∠COD=![]()
又∵∠COB=60°,
∴∠AOD=∠COD=60°,
∵OA=OD,
∴△AOD为等边三角形,
∴∠A=∠COB=60°,
∴OC∥AE,
∴∠OCE+∠E=180°
∵CE⊥AD,
∴∠E=90°,
∴∠OCE=90°,即OC⊥CE,
∵OC为⊙O的半径,
∴CE为⊙O的切线,
(2)由(1)知△AOD和△COD均为等边三角形,CE=![]() ,
,
∴OC=CD,∠OCD=60°,
∴∠ECD=90°﹣60°=30°,
∴cos∠ECD=![]() ,
,
∴CD=2,即⊙O的半径为2.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
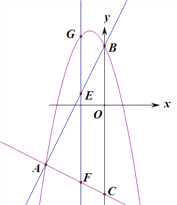
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有24个班,共1 000名学生,他们参加了一次数学测试.学校统计了所有学生的成绩,得到下列统计图.

(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和2.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
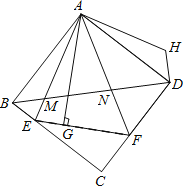
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3![]() ,求AG、MN的长.
,求AG、MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设快车离乙地的距离为y1(km),慢车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km).y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.则下列判断:①图1中a=3;②当x=![]() h时,两车相遇;③当x=
h时,两车相遇;③当x=![]() 时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=
时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=![]() h或
h或![]() h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com