
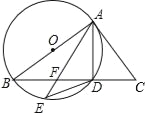
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC交于点F.
(1)求证:FD=CD;
(2)若AE=8,tan∠E=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)先利用切线的性质得出∠CAD+∠BAD=90°,再利用直径所对的圆周角是直角得出∠B+∠BAD=90°,从而可证明∠B=∠EAD,进而得出∠EAD=∠CAD,进而判断出△ADF≌△ADC,即可得出结论;(2)过点D作DG⊥AE,垂足为G.依据等腰三角形的性质可得到EG=AG=4,然后在Rt△GEG中,依据锐角三角函数的定义可得到DG的长,然后依据勾股定理可得到AD=ED=5,然后在Rt△ABD中,依据锐角三角函数的定义可求得AB的长,从而可求得⊙O的半径的长.
(1)∵AC 是⊙O 的切线,
∴BA⊥AC,
∴∠CAD+∠BAD=90°,
∵AB 是⊙O 的直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠CAD=∠B,
∵DA=DE,
∴∠EAD=∠E,
又∵∠B=∠E,
∴∠B=∠EAD,
∴∠EAD=∠CAD,
在△ADF和△ADC中,∠ADF=∠ADC=90°,AD=AD,∠FAD=∠CAD,
∴△ADF≌△ADC,
∴FD=CD.
(2)如下图所示:过点D作DG⊥AE,垂足为G.
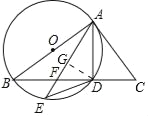
∵DE=AE,DG⊥AE,
∴EG=AG=![]() AE=4.
AE=4.
∵tan∠E=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得DG=4.
,解得DG=4.
∴ED=![]() =5.
=5.
∵∠B=∠E,tan∠E=![]() ,
,
∴sin∠B=![]() ,即
,即![]() ,解得AB=
,解得AB=![]() .
.
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】点P1(﹣1,y1),P2(2,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
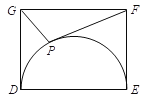
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
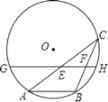
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为8,则GE+FH的最大值为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浙北商场一专柜销售某种品牌的玩具,每件进价为20元.销售过程中发现,每月销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似的看作一次函数:
(元)之间的关系可近似的看作一次函数:![]() .
.
(1)若每月销售260件,则每件利润是多少?
(2)如果该专柜想要每月获得2160元的利润,且成本要低.那么销售单价应定为多少元?
(3)设专柜每月获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润多少元?
(元),当销售单价定为多少元时,每月可获得最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,其部分图象如图所示. 对于此抛物线有如下四个结论:
,其部分图象如图所示. 对于此抛物线有如下四个结论:
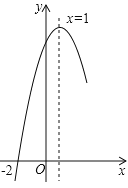
①![]() ;②
;②![]() ;
;
③若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点![]() 不在此抛物线上. 其中正确结论的序号是( )
不在此抛物线上. 其中正确结论的序号是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程![]() ,
,![]() 且
且![]() ,求
,求![]() 的值.
的值.
解:由![]() ,及
,及![]() ,可知
,可知![]() ,
,![]() .
.
又![]()
![]() ,
,
![]() .
.
![]()
![]() 可变形为
可变形为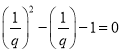 ,
,
根据![]() 和
和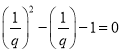 的特征.
的特征.
![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,
的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:![]() ,
,![]() 且
且![]() ,
,
(1)求:![]() 的值.
的值.
(2)求:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com