
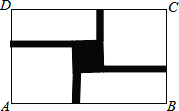
 如图,某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的$\frac{1}{4}$,若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$,求道路的宽.
如图,某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的$\frac{1}{4}$,若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$,求道路的宽.  阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(-1,2).
在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com