
【题目】一辆从A站开往D站的动车,途中经停B、C两站,互不相识的甲、乙、丙三人同时从A站上车。
(1)求甲、乙两人在同一车站下车的概率;
(2)甲、乙、丙三人在同一车站下车的概率为
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)用列举法列出甲、乙两人下车的所有可能结果,再看其中两人同一车站下车的可能结果,即可求出概率;
(2)同样地,用列举法列出甲、乙、丙三人下车的所有可能结果,再看其中三人同一车站下车的可能结果,即可求出概率.
(1)甲、乙两人下车的可能结果共有9种,即(B,B),(B,C),(B,D),(C,B),(C,C),(C,D),(D,B),(D,C),(D,D),每种结果出现的可能性相等.甲、乙两人在同一车站下车(记为事件1)的结果有3种,所以![]() ;
;
(2)甲、乙、丙三人下车的可能结果有27种,即(B,B,B),(B,B,C),(B,B,D),(B,C,B),(B,C,C),(B,C,D),(B,D,B),(B,D,C),(B,D,D),(C,B,B),(C,B,C),(C,B,D),(C,C,B),(C,C,C),(C,C,D),(C,D,B),(C,D,C),(C,D,D),(D,B,B),(D,B,C),(D,B,D),(D,C,B),(D,C,C),(D,C,D),(D,D,B),(D,D,C),(D,D,D),每种结果出现的可能性相等.甲、乙、丙三人在同一车站下车(记为事件k)的结果有3种,所以![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(﹣2,0)、B(6,0)两点.
与x轴交于A(﹣2,0)、B(6,0)两点.
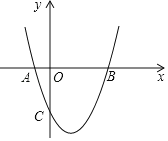
(1)求该抛物线的解析式;
(2)点P为y轴左侧抛物线上一个动点,若S△PAB=32,求此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以10元/千克的价格收购一批农产品进行销售,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 10 | 13 | 16 | 19 | 22 | |
日销售量y(千克) | 100 | 85 | 70 | 55 | 40 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定y与x之间的函数表达式;
(2)若该水果店要获得375元的日销售利润,销售单价x应定为多少元?
(3)该水果店应该如何确定这批水果的销售价格,才能使日销售利润W最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
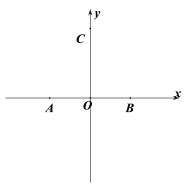
【题目】如图,在平面直角坐标系中,点A与点B关于原点O对称,点A![]() ,点C
,点C![]() ,点P在直线BC上运动.
,点P在直线BC上运动.
(1)连接AC、BC,求证:△ABC是等边三角形;
(2)求点P的坐标,使∠APO=![]() ;
;
(3)在平面内,平移直线BC,试探索:当BC在不同位置时,使∠APO=![]() 的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
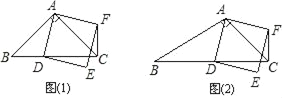
【题目】在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB≠AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=4![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
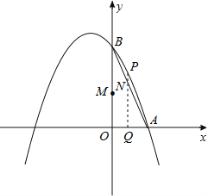
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防禽流感,上海建立了候鸟监测站,某候鸟监测站将一天7点至17点监测到上空飞过的候鸟数制成了如下直方图:
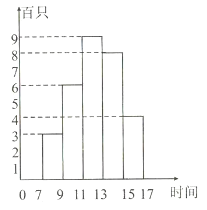
(1)候鸟飞过的高峰期在一天的______;
(2)这一天7点至17点期间,平均每小时飞过上空的候鸟有______只;
(3)每两个小时飞过上空的候鸟数的中位数是______;
(4)若一天飞过上空的候鸟数按此估算,该监测站九月份监测到的候乌只数约是______只;
(5)7时—9时段的频率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com