
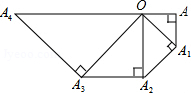
 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OAn的长度为$\sqrt{{2}^{n}}$.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OAn的长度为$\sqrt{{2}^{n}}$. 分析 利用等腰直角三角形的性质以及勾股定理分别求出各边长,进而得出答案.
解答 解:∵△OAA1为等腰直角三角形,OA=1,
∴AA1=OA=1,OA1=$\sqrt{2}$OA=$\sqrt{2}$;
∵△OA1A2为等腰直角三角形,
∴A1A2=OA1=$\sqrt{2}$,OA2=$\sqrt{2}$OA1=2;
∵△OA2A3为等腰直角三角形,
∴A2A3=OA2=2,OA3=$\sqrt{2}$OA2=2$\sqrt{2}$;
∵△OA3A4为等腰直角三角形,
∴A3A4=OA3=2$\sqrt{2}$,OA4=$\sqrt{2}$OA3=4.
∵△OA4A5为等腰直角三角形,
∴A4A5=OA4=4,OA5=$\sqrt{2}$OA4=4$\sqrt{2}$.
∵△OA5A6为等腰直角三角形,
∴A5A6=OA5=4$\sqrt{2}$,OA6=$\sqrt{2}$OA5=8.
∴OAn的长度为$\sqrt{{2}^{n}}$.
故答案为:$\sqrt{{2}^{n}}$.
点评 此题主要考查了等腰直角三角形的性质以及勾股定理,熟练应用勾股定理得出是解题关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
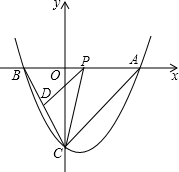 如图,抛物线y=$\frac{1}{2}{x^2}$-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
如图,抛物线y=$\frac{1}{2}{x^2}$-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
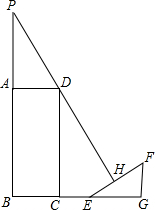 如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).
如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | 16 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com