Question

1．如图，已知点P为∠AOB的角平分线上的一定点，D是射线OA上的一定点，E是OB上的某一点，满足PE=PD，则∠OEP与∠ODP的数量关系是∠OEP=∠ODP或∠OEP+∠ODP=180°．

Answer 1

分析 以O为圆心，以OD为半径作弧，交OB于E₂，连接PE₂，根据SAS证△E₂OP≌△DOP，推出E₂P=PD，得出此时点E₂符合条件，此时∠OE₂P=∠ODP；以P为圆心，以PD为半径作弧，交OB于另一点E₁，连接PE₁，根据等腰三角形性质推出∠PE₂E₁=∠PE₁E₂，求出∠OE₁P+∠ODP=180°即可．

解答 解：∠OEP=∠ODP或∠OEP+∠ODP=180°，理由如下：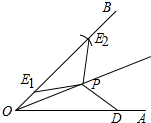
以O为圆心，以OD为半径作弧，交OB于E₂，连接PE₂，如图所示：
∵在△E₂OP和△DOP中，$\left\{\begin{array}{l}{O{E}_{2}=OD}&{\;}\\{∠{E}_{2}OP=∠DOP}&{\;}\\{OP=OP}&{\;}\end{array}\right.$，
∴△E₂OP≌△DOP（SAS），
∴E₂P=PD，
即此时点E₂符合条件，此时∠OE₂P=∠ODP；
以P为圆心，以PD为半径作弧，交OB于另一点E₁，连接PE₁，
则此点E₁也符合条件PD=PE₁，
∵PE₂=PE₁=PD，
∴∠PE₂E₁=∠PE₁E₂，
∵∠OE₁P+∠E₂E₁P=180°，
∵∠OE₂P=∠ODP，
∴∠OE₁P+∠ODP=180°，
∴∠OEP与∠ODP所有可能的数量关系是：∠OEP=∠ODP或∠OEP+∠ODP=180°，
故答案为：∠OEP=∠ODP或∠OEP+∠ODP=180°．

点评 本题考查了全等三角形的性质和判定，等腰三角形的性质和判定等知识点，主要考查学生的猜想能力和分析问题和解决问题的能力，题目具有一定的代表性，是一道比较好的题目．