
【题目】如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.
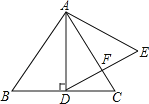
(1)求△ABC的周长;
(2)判断AC、DE的位置关系,并给出证明.
【答案】(1)12;(2)AC⊥DE,理由见解析
【解析】
(1)根据等边三角形的性质求得BD=CD=2,即可求得BC=4,所以△ABC为边长为4的正三角形,从而求出三角形的周长;
(2)根据等边三角形的性质求得∠C=∠ADE=60°,再求出∠CDE=30°,从而得到∠CFD=90°即可得出结论.
解:(1)∵在等边△ABC中,AD⊥BC,BD=2,
∴BD=CD=2,
∴BC=BD+CD=4,
∴等边△ABC的周长为:AB+BC+CA=3BC=12;
(2)AC、DE的位置关系:AC⊥DE.
∵△ABC和△ADE是等边三角形,
∴∠C=60°,∠ADE=60°,
∵AD⊥BC,
∴∠ADC=90°,
在△CDF中,∵∠CDE=90°﹣∠ADE=30°,
∴∠CFD=180°﹣∠C﹣∠CDE=180°﹣60°﹣30°=90°.
∴AC⊥DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
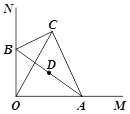
【题目】如图,在Rt△ABC中,BC![]() 2,∠BAC
2,∠BAC![]() 30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA
30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA![]() ;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为
;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为![]() .
.
其中正确的是( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BE平分∠ABC,DE∥BC.
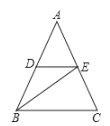
(1)试猜想△BDE的形状,并说明理由;
(2)若∠A=35°,∠C=70°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
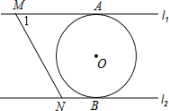
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() ,点
,点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移,若
平移,若![]() 的半径为
的半径为![]() ,
,![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A. ![]() 和
和![]() 的距离为
的距离为![]() B. 当
B. 当![]() 与
与![]() 相切时,
相切时,![]()
C. ![]() D. 当
D. 当![]() 时,
时,![]() 与
与![]() 相切
相切
查看答案和解析>>
科目:初中数学 来源: 题型:
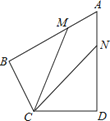
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
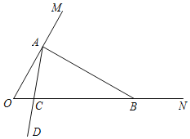
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为 °,△AOB (填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
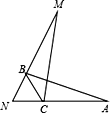
【题目】如图,点B,C分别在线段NM,NA上,在△ABC中,∠A∶∠ABC∶∠BCA=3∶5∶10,且△ABC≌△MNC,则∠BCM∶∠NBA等于( )
A.1∶2B.1∶3C.1∶4D.1∶5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
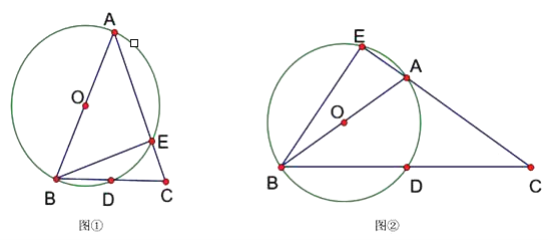
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com