
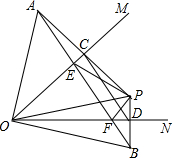
 如图,∠MON=45°,点P在∠MON内,OP=4,分别作点P关于OM、ON的对称点A、B,PA、PB分别交OM、ON于点C、D,连接AB分别交OM、ON于点E、F.
如图,∠MON=45°,点P在∠MON内,OP=4,分别作点P关于OM、ON的对称点A、B,PA、PB分别交OM、ON于点C、D,连接AB分别交OM、ON于点E、F.分析 (1)由轴对称图形的性质可知AC=PC,AE=PE,PD=DB,PF=FB,最后依据两点之间线段最短即可得出答案;
(2)由题意可知△AOB为等腰直角三角形,然后依据三角形的面积公式求解即可.
解答 解:(1)由轴对称的性质可知:AC=PC,AE=PE,PD=DB,PF=FB,
∴PC+CD+DP=AC+CD+DB,PE+EF+FP=AE+EF+FB.
∵AC+CD+DB>AE+EF+FB,
∴PC+CD+DP>PE+EF+FP.
(2)由轴对称的性质可知;OP=OB=OA=4,∠AOM=∠MOP,∠BON=∠PON.
∵∠MON=45°,
∴∠AOB=2∠MON=2×45°=90°.
∴${S}_{△AOB}=\frac{1}{2}×4×4$=8.
故答案为:(1)>;(2)8.
点评 本题主要考查的是轴对称的性质,依据轴对称图形的性质找出相等的角和相等的线段是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com