

分析 (1)根据点的坐标和新定义解答即可;
(2)根据直线y=x+b的特点,结合SM=2,根据等腰直角三角形的性质解答;
(3)根据T在⊙O内,确定ST的范围,根据给出的条件、结合图形求出满足条件的线段PQ长度的最大值.
解答 解:(1)∵点B(1,0),
∴SB=0,
∵C(1,1),
∴SC=$\sqrt{2}$-1,
∵$D({0,\frac{1}{3}})$,
∴SD=$\frac{2}{3}$,
故答案为:0;$\sqrt{2}$-1;$\frac{2}{3}$;
(2)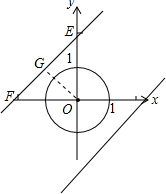 设直线y=x+b与分别与x轴、y轴交于F、E,
设直线y=x+b与分别与x轴、y轴交于F、E,
作OG⊥EF于G,
∵∠FEO=45°,
∴OG=GE,
当OG=3时,GE=3,
由勾股定理得,OE=3$\sqrt{2}$,
此时直线的解析式为:y=x+3$\sqrt{2}$,
∴直线y=x+b上存在点M,使得SM=2,b的取值范围是-3$\sqrt{2}$≤b≤3$\sqrt{2}$;
(3)∵T在⊙O内,
∴ST≤1,
∵ST≥SR,
∴SR≤1,
∴线段PQ长度的最大值为1+2+1=4.
点评 本题考查的是等腰直角三角形的性质、新定义、点与圆的位置关系,正确理解点P到⊙O的距离SP的定义、灵活运用数形结合思想是解题的关键.


科目:初中数学 来源: 题型:填空题
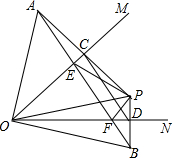 如图,∠MON=45°,点P在∠MON内,OP=4,分别作点P关于OM、ON的对称点A、B,PA、PB分别交OM、ON于点C、D,连接AB分别交OM、ON于点E、F.
如图,∠MON=45°,点P在∠MON内,OP=4,分别作点P关于OM、ON的对称点A、B,PA、PB分别交OM、ON于点C、D,连接AB分别交OM、ON于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
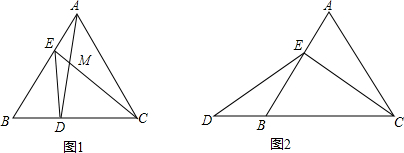
 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
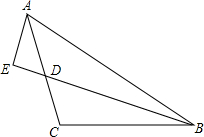 如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.
如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com