
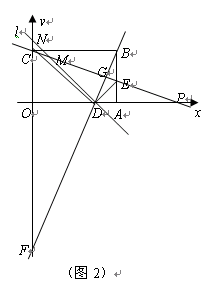
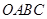 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点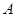 在
在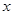 轴上,点
轴上,点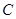 在
在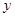 轴上,将边
轴上,将边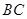 折叠,使点
折叠,使点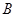 落在边
落在边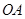 的点
的点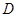 处.已知折叠
处.已知折叠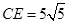 ,且
,且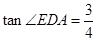 .
.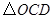 与
与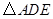 是否相似?请说明理由;
是否相似?请说明理由; 与
与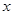 轴交点
轴交点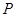 的坐标;
的坐标;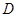 的直线
的直线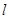 ,使直线
,使直线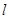 、直线
、直线 与
与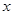 轴所围成的三角形和直线
轴所围成的三角形和直线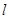 、直线
、直线 与
与 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.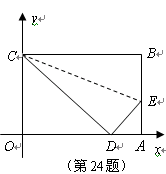
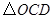 与
与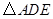 相似.
相似.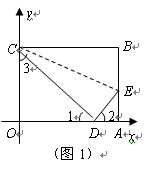
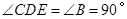 ,
,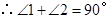 ,
,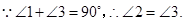
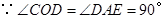 ,
,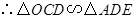 .
.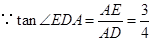 ,
, 设
设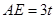 ,
,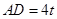 .
.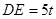 .
.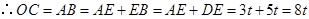 .
.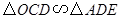 ,得
,得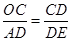 ,
,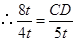 ,
,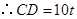 .
.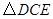 中,
中,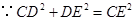 ,
,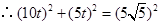 ,解得
,解得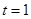 .
.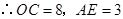 ,点
,点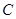 的坐标为
的坐标为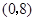 ,
, 的坐标为
的坐标为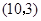 ,
, 的解析式为
的解析式为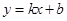 ,
,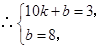 解得
解得
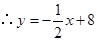 ,则点
,则点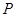 的坐标为
的坐标为 .
. 有2条:
有2条: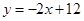 ,
,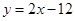 .
.
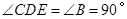 ,根据同角的余角相等可得
,根据同角的余角相等可得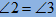 ,再有
,再有 即可得到
即可得到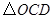 与
与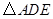 相似;
相似;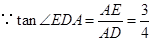 ,
, 设
设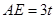 ,则
,则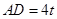 ,由勾股定理得
,由勾股定理得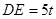 ,
,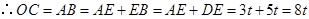 ,由(1)
,由(1)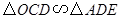 ,根据对应边成比例可得
,根据对应边成比例可得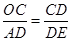 ,
,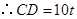 ,在
,在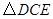 中根据勾股定义即可求出
中根据勾股定义即可求出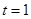 ,从而得到点
,从而得到点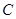 、点
、点 的坐标,再根据待定系数法即可得到直线
的坐标,再根据待定系数法即可得到直线 的解析式,从而得到点
的解析式,从而得到点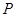 的坐标。
的坐标。

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, ,
, ,
, 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形 的高.
的高. ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的边长为6,菱形
的边长为6,菱形 的三个顶点
的三个顶点 分别在正方形
分别在正方形 边
边 上,
上, ,连接
,连接 .
. 时,求
时,求 的面积;
的面积; ,用含
,用含 的代数式表示
的代数式表示 的面积;
的面积; 的面积能否等于
的面积能否等于 ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com