
【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
【答案】(1)80分,80分 ;(2)80分; (3)9.33,11.33 ;(4)派甲去.
【解析】试题分析:本题考查了方差, 算术平均数, 中位数的计算.
(1)由平均数的计算公式计算甲、乙测试成绩的平均分;
(2)将一组数据从小到大(或从大到小)重新排列后,中间两个数的平均数是甲、乙测试成绩的中位数;
(3)由方差的计算公式计算甲、乙测试成绩的方差;
(4)方差越小,表明这个同学的成绩偏离平均数越小,即波动越小,成绩越稳定.
解:(1)x甲=![]() (分),
(分),
x乙=![]() (分).
(分).
(2)甲、乙测验成绩的中位数都是80分.
(3) ![]() =
=![]() [(79-80)2+(78-80)2+(84-80)2+(81-80)2+(83-80)2+(75-80)2]≈9.33,
[(79-80)2+(78-80)2+(84-80)2+(81-80)2+(83-80)2+(75-80)2]≈9.33,
![]() =
=![]() [(83-80)2+(77-80)2+(80-80)2+(85-80)2+(80-80)2+(75-80)2]≈11.33.
[(83-80)2+(77-80)2+(80-80)2+(85-80)2+(80-80)2+(75-80)2]≈11.33.
(4)结合以上信息,应该派甲去,因为在平均数和中位数都相同的情况下,甲的测验成绩更稳定.


科目:初中数学 来源: 题型:
【题目】如图①,A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,且AB=CD.
(1)求证:BD平分EF.
(2)若将△DEC的边EC沿AC方向移动变为图②,其余的条件不变,上述结论是否仍成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,世界上能制造出的最小晶体管的长度只有0.000 000 04m,将0.000 000 04用科学记数法表示为( )
A.4×108
B.4×10﹣8
C.0.4×108
D.﹣4×108
查看答案和解析>>
科目:初中数学 来源: 题型:
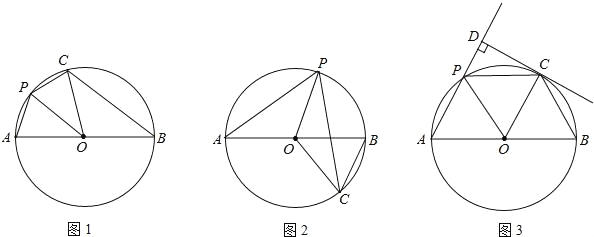
【题目】已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com