
如图1,抛物线y=nx2-11nx+24n (n<0) 与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.
(1)填空:点B的坐标为(_ ),点C的坐标为(_ );
(2)连接OA,若△OAC为等腰三角形.
①求此时抛物线的解析式;
②如图2,将△OAC沿x轴翻折后得△ODC,点M为①中所求的抛物线上点A与点C两点之间一动点,且点M的横坐标为m,过动点M作垂直于x轴的直线l与CD交于点N,试探究:当m为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
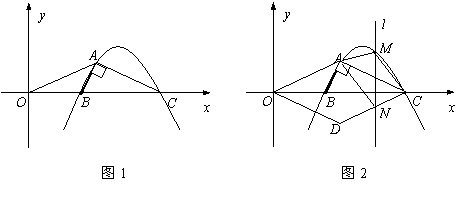 |
解:(1)B(3,0),C(8,0)
(2)①作AE⊥OC,垂足为点E
∵△OAC是等腰三角形,∴OE=EC=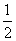 ×8=4,∴BE=4-3=1
×8=4,∴BE=4-3=1
又∵∠BAC=90°,∴△ACE∽△BAE,∴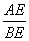 =
=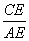
∴AE2=BE·CE=1×4,∴AE=2
∴点A的坐标为 (4,2)
把点A的坐标 (4,2)代入抛物线y=nx2-11nx+24n,得n=-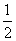
∴抛物线的解析式为y=-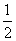 x2+
x2+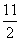 x-12
x-12
②∵点M的横坐标为m,且点M在①中的抛物线上
∴点M的坐标为 (m,-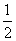 m2+
m2+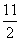 m-12),由①知,点D的坐标为(4,-2),
m-12),由①知,点D的坐标为(4,-2),
则C、D两点的坐标求直线CD的解析式为y=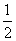 x-4
x-4
∴点N的坐标为 (m,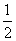 m-4)
m-4)
∴MN=(-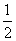 m2+
m2+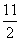 m-12)-(
m-12)-(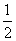 m-4)=-
m-4)=-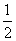 m2+5m-8
m2+5m-8
∴S四边形AMCN=S△AMN+S△CMN=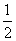 MN·CE=
MN·CE=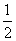 (-
(-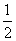 m2+5m-8)×4
m2+5m-8)×4
=-(m-5)2+9
∴当m=5时,S四边形AMCN=9


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
若(x+a)(x-2)=x2+bx-6对于x的任何值都成立,则a,b的值为( )
A.a=3,b=5 B.a=3,b=1 C.a=-3,b=-1 D.a=-3,b=-5
查看答案和解析>>
科目:初中数学 来源: 题型:
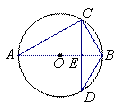
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结 论中不成立的是( )
论中不成立的是( )
A.∠A﹦∠D B.CE﹦DE
C.∠ACB﹦90° D.CE﹦BD
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com