
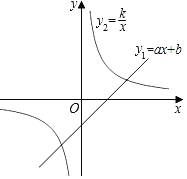
【题目】如图,已知一次函数y1=ax+b(a≠0)与反比例函数y2=![]() (k>0),两函数图象交于(4,1),(﹣2,n)两点.
(k>0),两函数图象交于(4,1),(﹣2,n)两点.
(1)求a,k的值;
(2)若y2>y1>0,求x的取值范围.
【答案】(1)a=![]() ,k=4;(2)2<x<4.
,k=4;(2)2<x<4.
【解析】
(1)先把(4,1)代入y2=![]() 求出k确定反比例函数解析式,再利用反比例函数解析式求出n,然后根据待定系数法求一次函数解析式,即可求出a的值;
求出k确定反比例函数解析式,再利用反比例函数解析式求出n,然后根据待定系数法求一次函数解析式,即可求出a的值;
(2)在第一象限内,写出反比例函数图像在一次函数图像上方所对应的自变量的范围即可.
解:(1)把(4,1)代入y2=![]() 得k=4×1=4,
得k=4×1=4,
∴反比例函数解析式为y2=![]() ,
,
把(﹣2,n)代入y2=![]() 得﹣2n=4,解得n=﹣2,
得﹣2n=4,解得n=﹣2,
把(4,1),(﹣2,﹣2)代入y1=ax+b得![]() ,解得
,解得 ,
,
∴一次函数解析式为y1=![]() x﹣1,
x﹣1,
∴a=![]() ,k=4;
,k=4;
(2)当![]() x﹣1=0,解得x=2,则一次函数y1=ax+b(a≠0)图像与x轴的交点为(2,0),根据函数图像可得:当2<x<4时,y2>y1>0.
x﹣1=0,解得x=2,则一次函数y1=ax+b(a≠0)图像与x轴的交点为(2,0),根据函数图像可得:当2<x<4时,y2>y1>0.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】 如图,在△ABC中,DE是边AB的垂直平分线,分别交边AB,AC于点D,E,连接BE,点F在边AC上,AB=AF,连接BF.
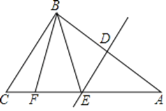
(1)求证:∠BEC=2∠A;
(2)当∠BFC=108°时,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:
①16a+4b+c>0:
②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1<y2;
,y2)是函数图象上的两点,则y1<y2;
③c=3a;
④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .
.
其中正确的有_____.(请将正确结论的序号全部填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进消费,杭州市政府开展发放政府补贴消费的“消费券”活动,一超市的月销售额逐步增加.据统计,2月份销售额为200万元,4月份销售额为500万元.若3,4月平均每月的增长率为x,则( )
A.200(1+x)=500B.200(1+x)+200+(1+x)2=500
C.200(1+x)2=500D.200+200(1+x)+200(1+x)2=500
查看答案和解析>>
科目:初中数学 来源: 题型:
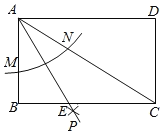
【题目】如图,矩形ABCD中∠BAC=60°,以点A为圆心,以任意长为半径作弧分别交AB,AC于点M,N两点,再分别以点M,N为圆心,以大于![]() MN的长为半径作弧交于点P,作射线AP交BC于点E,若BE=2cm,则CE的长为( )
MN的长为半径作弧交于点P,作射线AP交BC于点E,若BE=2cm,则CE的长为( )
A.6cmB.6![]() cmC.4cmD.4
cmC.4cmD.4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
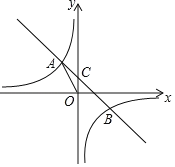
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,5),点B的坐标为(5,n),tan∠AOC
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,5),点B的坐标为(5,n),tan∠AOC![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
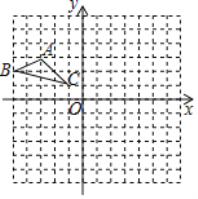
【题目】△ABC在边长为l的正方形网格中如图所示.
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某项比赛中,已知不同小组的甲、乙两队的五次预选赛成绩(每次比赛的成绩为0分,10分,20分三种情况)分别如下列不完整的统计表及条形统计图所示.
甲队五次预选赛成绩统计表
比赛场次 | 1 | 2 | 3 | 4 | 5 |
成绩(分) | 20 | 0 | 20 | x | 20 |
乙队五次预选赛成绩条形统计图
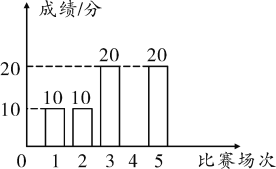
已知甲、乙两队五次预选赛成绩的众数相同,平均数也相同.
(1)求出乙第四次预选赛的成绩;
(2)求甲队成绩的平均数及x的值;
(3)从甲、乙两队前3次比赛中随机各选择一场比赛的成绩进行比较,求选择到的甲队成绩优于乙队成绩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com